Решение типовых задач. Задача 3.1. Система состоит из трех устройств

Задача 3.1. Система состоит из трех устройств. Интенсивность отказов электронного устройства равна λ ₁=0, 16*10^-3 1/час = const. Интенсивности отказов двух электромеханических устройств линейно зависят от времени и определяются следующими формулами

λ ₂=0, 23*10^-4t 1/час, λ ₃=0, 06*10^-6t^{2, 6} 1/час.

Необходимо рассчитать вероятность безотказной работы изделия в течение 100 час.

Решение. На основании формулы (3.3) имеем

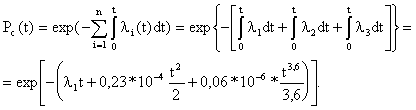
Для t=100 час

.

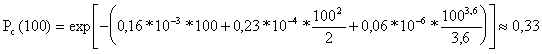Задача 3.2. Система состоит из трех блоков, среднее время безотказной работы которых равно: m_t1=160 час; m_t2 =320 час; m_t3 = 600 час.

Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднее время безотказной работы системы.

Решение. Воспользовавшись формулой (3.17) получим

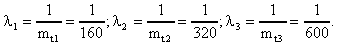
Здесь λ _i - интенсивность отказов i -го блока. На основании формулы (3.11) имеем

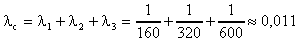1/час.

Здесь λ _c - интенсивность отказов системы.

На основании формулы (3.16) получим:

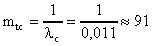час.

Задача 3.3. Система состоит из 12600 элементов, средняя интенсивность отказов которых λ _ср=0, 32*10^-6 1/час. Требуется определить P_c(t), q_c(t), f_c(t), m_tc, для t=50 час.

Здесь P_c(t) - вероятность безотказной работы системы в течение времени t;

q_c(t) - вероятность отказа системы в течение времени t;

f_c(t) - частота отказов или плотность вероятности времени T безотказной работы системы;

m_tс - среднее время безотказной работы системы.

Решение. Интенсивность отказов системы по формуле (3.11) будет

λ _с = λ _ср*n = 0, 32*10^-6*12600 = 4, 032*10^-3 1/час.

Из (3.13) имеем

Р_с(t) = e^{- λ сt}; Р_с(50) = e^{-4, 032*0, 001*50 0}, 82.

Из (3.15) получим

q_c(t)= 1- P_c(t) = λ _с P_c(t); q_c(50)=1-P_c(50) 0, 18.