
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для пытливых
|
|
6. Исследуйте влияние на спектры импульсных сигналов длительности их фронта и среза. Как они влияют на ширину спектра сигнала?
7. Проведите имитационное моделирование в программах MicroCAP или WorkBench спектров произвольных сигналов, например, последовательностей прямоугольных импульсов.
8. Создайте модель фильтра нижних (верхних) частот и проанализируйте изменения спектров проходящих через нее сигналов (прямоугольных импульсов).
9. Проведите численные расчеты спектров рассмотренных в лабораторной работе сигналов в программе MathCAD.
МОДЕЛИРОВАНИЕ СПЕКТРОВ ПЕРИОРДИЧЕСКИХ СИГНАЛОВ
Исследуйте спектры амплитуд сигналов при прохождении последовательности прямоугольных импульсов через фильтрующие цепи. Применительно к RC фильтру нижних частот модель представлена на рис. 30.
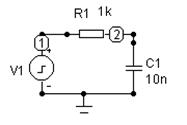
Рис. 30
Проанализируйте частотные характеристики цепи и временные диаграммы сигналов на входе и выходе.
Сравните спектры амплитуд входного и выходного сигналов, проанализируйте влияние параметров цепи, сделайте соответствующие выводы.
Объясните характер наблюдаемых спектров и их отличие от теоретического вида. Как форма спектров связана с длиной реализации сигнала, частотой квантования (этот вопрос выходит за рамки курса ОТЦ)?
Аналогично рассмотрите прохождение того же сигнала через простейший RC фильтр верхних частот и последовательный RLC колебательный контур, проведите анализ результатов моделирования. Соответствующие модели показаны на рис. 31 и 32 соответственно.
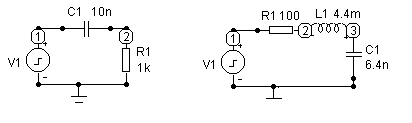
Рис. 31 Рис. 32
Проведите исследования спектров сигналов с использованием программы MATHCAD на базе функции fft.
Функция fft(u) реализует быстрое преобразование Фурье (БПФ) вида
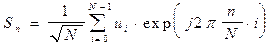 ,
,
где ui – отсчеты сигнала u(t) в моменты времени ti=i´ Dt, i – номер отсчета, Dt – интервал дискратизации сигнала по времени на периоде колебаний T=N´ Dt, N = 2m – число отсчетов на периоде сигнала (m – целое число), Sn – результат БПФ, комплексное число, определяющее n-ю гармонику сигнала.
Постоянная составляющая спектра сигнала U0 равна
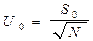 ,
,
а амплитуда n-й гармоники Un и ее начальная фаза yn определяются выражениями:
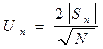 ,
,
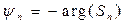 .
.
Изменяя параметры сигнала, исследуйте их влияние на спектры амплитуд и фаз, сравните результаты с полученными с помощью пакета MICROCAP.
С помощью пакета MATHCAD рассмотрите влияние изменения амплитуд и начальных фаз гармоник последовательности прямоугольных импульсов на форму временной диаграммы.