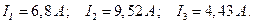Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет токов в ветвях методом контурных токов
|
|
Предварительно представим эдс и сопротивления ветвей в комплексной форме:
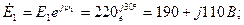

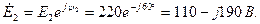
Здесь 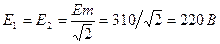 - действующие значение эдс.
- действующие значение эдс.
Комплексные сопротивления ветвей.
z 1 = R 1 – jx 1 = 10 – j 32 = 33, 5 · e - j 72º 39′ Ом;
z 2 = R 2 + j x 2 = 15 + j 8 = 17 ej 28°04′ Ом;
z 3 = R 3 + j (x 3 – x 4) = 5 + j (22 – 10) = 13 ej 67°38′ Ом.
Эквивалентная расчетная схема представлена на рис. 3.3.
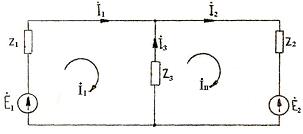
Рис. 3.3. Расчетная схема для МКТ
Схема имеет два смежных контура. Следовательно, по методу контурных токов нужно составить два уравнения. Зададимся произвольно направлениями контурных токов (в контурах удобно направлять их одинаково, например, по часовой стрелке) и составим для них уравнения по второму закону Кирхгофа:
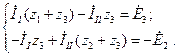
Здесь сопротивление первого контура
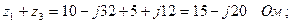
сопротивление второго контура
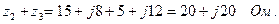
Сопротивление ветви, смежной для I-го и П-го контуров,
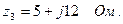
Подставляя значения сопротивлений и эдc в (3.1), получим

Систему уравнений (3.2) проще рассчитать на ЭВМ, пользуясь комплексом программ с комплексными коэффициентам (КС) (см. инструкцию с. З6).
Для расчета системы уравнений (3.2) с помощью программа " матрица", или используя комплекс программ с действительными коэффициентами (ДС), необходимо выполнить следующие алгебраические преобразования. Комплексы контурных токов запишем в алгебраической форме
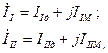
где II д и III д - действительные составлявшие комплексов контурных токов 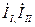 ;
;
IIM и IIIM - мнимые составляющие комплексов контурных токов. Подставим эти токи в систему уравнений (3.1), одновременно сделав подстановку числовых значений сопротивлений и эдс:
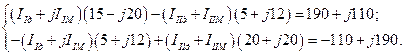 (3.3)
(3.3)
Раскроем скобки:
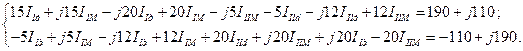
Далее, используя известное свойство комплексных чисел, - два комплексных числа равны, если соответственно равны их вещественные и мнимые части, - запишем систему уравнений в следующем виде:
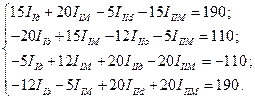
Для решения полученной системы уравнений на ЭBM составим матрицу из коэффициентов при действительных и мнимых составляющих токов и свободных членов. Матрица имеет вид
II д IIM III д IIIM E
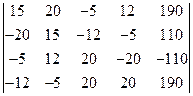 (3.6)
(3.6)
Введя матрицу в ЭВМ (см. инструкцию с. З6), получаем следующие результаты:
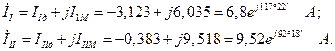
Действительные токи ветвей связаны с контурными токами следующим образом (см. рис. 3.3):
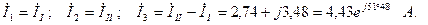
При определении тока 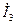 из большего по модулю контурного тока
из большего по модулю контурного тока 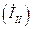 вычитаем меньший контурный ток
вычитаем меньший контурный ток 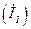 и направляем ток
и направляем ток 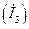 по направлению большего контурного тока
по направлению большего контурного тока 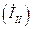 .
.
Действующие значения токов: