
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Маршруты, цепи, циклы. Длина маршрута.
|
|
Маршрутом в графе G называется чередующаяся последовательность вершин и ребер: v0, l 1, v1, l 2, …, lk, vk, в которой любые два соседних элемента инцидентны. Это определение подходит и для псевдо и мультиграфов. В орграфе достаточно указать только последовательность вершин (узлов) или только последовательность ребер (дуг) если v0=vk, то маршрут называется замкнутым, если нет, то открытым.
Если все ребра различны, то маршрут называется цепью, если все вершины различны, то маршрут называется простой цепью В цепи v0 и vk называются концами цепи; цепь соединяющая вершины u и v обозначают < u, v>; замкнутая цепь называется циклом; простая замкнутая цепь прстым циклом. Граф без циклов называется ациклическим.
Для орграфов цепь называется путем, а цикл – контуром.
Пример 1.
v1 v2
1º v1, v3, v1, v4 – маршрут, но не цепь.
2º v1, v3, v5, v2, v3, v4 – цепь, но не простая (т.к. не все
v3 вершины различны, а различны рёбра)
3º v1, v4, v3, v2, v5 – простая цепь, но не цикл (т.к. не
v4v5 замкнута)
4º v1, v3, v5, v2, v3, v4, v1 – но не простой (т.к. цепь не простая хотя, замкнутая)
5º v1, v3, v4, v1 – простой цикл (все ребра и все вершины различны)
Длиной маршрута называется количество ребер в нем (с повторениями).
Пример 2.
Дан граф G, в нем:
1 2 (1, 2), (1, 2, 4, 7), (3, 4, 5, 6) – простые цепи
(3, 4, 5, 6) – цепь простая, но не ЦИК
3 4 5 6
(1, 2, 4, 7, 8, 4) – не простая цепь (есть одинаковые
вершины)
7 8 (1, 2, 4, 7, 8, 4, 1) – цикл, но не простой.
Пусть G – граф, возможно ориентированный. Маршрут называется путём, если все его дуги различны. Путь называется контуром, если v0=vk. Вершина v называется достижимой из вершины u, если 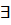 < u, v> путь. Расстоянием между вершинами называется длина кратчайшей цепи < u, v>
< u, v> путь. Расстоянием между вершинами называется длина кратчайшей цепи < u, v>
Пример 3.
2 4 5
1 3
Контур (1, 2, 3)
Вершина 5 достижима из любой вершины; из вершины 5 недостижима ни одна из остальных вершин