Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коэффициент ассоциации и контингенции.
|
|
При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативного признака, используют коэффициент ассоциации или коэффициент контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным (например, высокий - низкий, хороший - плохой и т.д.).
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
Коэффициенты вычисляются по формулам:
Ассоциации: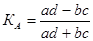 
Контингенции: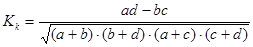 
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь подтверждается если Ka³ 0, 5 или KK³ 0, 3.
Например, необходимо оценить наличие связи между работниками организации, распределениями по полу и содержанию работы. Результаты исследований приведены в таблице.
| Работа | Мужчины | Женщины | Всего |
| Интересная | 300 (а) | 201 (b) | |
| Неинтересная | 130 (с) | 252 (d) | |
| Итого |
Коэффициент ассоциации (КA) определяется по формуле:
В тех случаях, когда хотя бы один из четырех показателей в «таблице четырех полей» отсутствует, величина коэффициента ассоциации будет равна единице, что дает преувеличенную оценку степени тесноты связи между признаками, и предпочтение следует отдать коэффициенту контингенции (КK):
Т.о. можно сделать вывод, что содержание работы не зависит от пола работника.
Если каждый из качественных признаков состоит из большого числа групп (более двух), то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова. Для данных коэффициентов необходимо составить таблицу взаимной сопряженности:
| X\Y | I | II | III | Всего |
| I | nxy | nx | ||
| II | nx | |||
| III | nx | |||
| Итого | ny | ny | ny | n |
; 
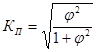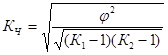
где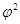 
-показатель взаимной сопряженности 
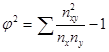; nxy- частота каждой клетки таблицы взаимной сопряженности; nx, ny -итоговые частоты соответствующих строк и столбцов; К1 , К2 –число строк и столбцов..
В качестве примера исследуем связь между качеством и себестоимостью услуг электросвязи.
| Качество услуг | Себестоимость услуг | Итого обследованных организаций | ||
| Низкая | Средняя | Высокая | ||
| Низкое | 23 (13) | 13 (17) | 14 (20) | |
| Среднее | 10 (13) | 25 (17) | 15 (20) | |
| Высокое | 7 (13) | 12 (17) | 31 (20) | |
| Итого |
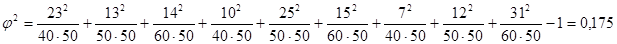
Тогда коэффициенты взаимной сопряженности Пирсона и Чупрова равны:
КП=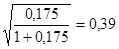 
; КЧ= 
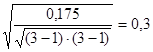и свидетельствуют о наличие умеренной связи между уровнями качества и себестоимости услуг электросвязи.
Чем ближе величины КП и КЧ к 1, тем теснее связь.
Коэффициенты взаимной сопряженности Пирсона и Чупрова можно вычислить используя критерий «хи-квадрат». Если признак, положенный в основу группировки по строкам таблицы (качество услуг), не зависит от признака, положенного в основу группировки по столбцам (себестоимость услуг), то в каждой строке (столбце) распределение частот должно быть пропорционально распределению их в итоговой строке (столбце). Такое распределение можно рассматривать в известной мере в качестве теоретического.
f11=40*50/150=13; f12=50*50/150=17; f13=60*50/150=20
f21=40*50/150=13; f22=50*50/150=17; f33=60*50/150=20
f31=40*50/150=13; f32=50*50/150=17; f33=60*50/150=20
Расчетное значение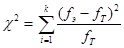 
Где fэ и fТ соответствующие эмпирические и теоретические частоты. К –число групп
Тогда
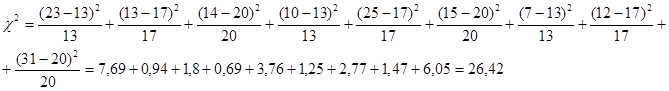
На основе критерия «хи-квадрат» определяются показатели степени тесноты связи — коэффициенты взаимной сопряженности К. Пирсона и А. Чупрова. Коэффициент взаимной сопряженности К, Пирсона рассчитывается по формуле:
= 
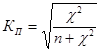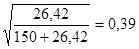
где п — общее число наблюдений:
Коэффициент взаимной сопряженности А. Чупрова позволяет учесть число групп по каждому признаку и определяется следующим образом:
= 
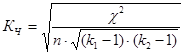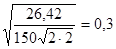
где К1 и К2 –число строк и столбцов в таблице, n –число наблюдений.
Если требуется оценить тесноту связи между альтернативным и количественным признаками, то рассчитывается биссериальный коэффициент корреляции:
где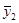 
и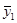 
-средние в группах; 
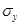-среднее квадратическое отклонение фактических значений признака от среднего уровня; p- доля первой группы, q – доля второй группы; Z- табличные значения z-распределения в зависимости от p.
В качестве примера рассмотрим зависимость уровня доходов работников организации связи от уровня специального образования.
| Уровень образования | Уровень доходов, тыс. руб. | Всего | ||
| 6-10 (8) | 10-14 (12) | 14-18 (16) | ||
| Имеют специальное высшее образование | ||||
| Не имеют специального образования | ||||
| Итого |
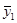=(8*5+12*10+16*15)/30=13, 3 тыс. руб.
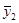=(8*10+12*6+16*4)/20=10, 8 тыс. руб.
=(8*15+12*16+16*19)/50=12, 3 тыс. руб.
= 
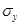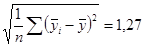; p=30/50=0, 6; q=20/50=0, 4
Zтабл=0, 4973
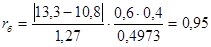
Величина биссериального коэффициента корреляции доказывает, что уровень доходов работников тесно связан с наличием специального образования.