Линейный коэффициент корреляции.

Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции (r), который был предложен английским ученым К. Пирсоном.

При расчете этого показателя учитываются не только знаки отклонений индивидуальных значений признака от средней, но и сама величина таких отклонений, т.е. соответственно для факторного и результативного признаков определяют величины (x_i, - 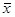) и (у_i - ).

Сравнению могут подлежать нормированные отклонения, выраженные в относительных величинах, т.е. в долях среднего квадратического отклонения. Так, для факторного признака будем иметь совокупность величин

Полученные нормированные отклонения можно сравнивать между собой. Для того чтобы получить обобщающую характеристику степени тесноты связи между признаками для всей совокупности, рассчитывают среднюю величину произведений нормированных отклонений. Полученная таким образом средняя и будет являться линейным коэффициентом корреляции (г):

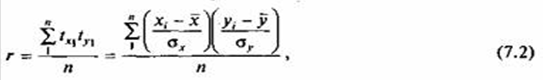
Или

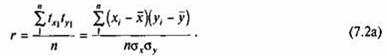
Вычисление коэффициента корреляции по формуле (7.2) является достаточно трудоемкой операцией. Выполнив несложные преобразования, можно получить следующую формулу для расчета линейного коэффициента корреляции:

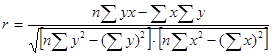
При пользовании этой формулой отпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что исключает ошибку в расчетах при округлении средних величин.

Линейный коэффициент корреляции изменяется в пределах от -1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак указывает на направление связи: прямой зависимости соответствует знак «плюс», а обратной зависимости — знак «минус».

Используем данные табл. 5 и рассчитаем линейный коэффициент корреляции:

, ,

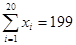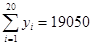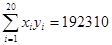
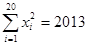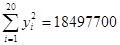, , тогда,

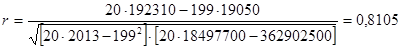
Полученная величина линейного коэффициента корреляции свидетельствует о возможном наличии достаточно тесной прямой зависимости между рассматриваемыми признаками.