Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению и аналитическому выражению.
|
|
По степени тесноты связи различают количественные критерии оценки тесноты связи.
Количественные критерии оценки тесноты связи Таблица 1
| Величина коэффициента | Характер связи |
| До ± 0, 3 | Практически отсутствует |
| ± 0, 3 - ± 0, 5 | Слабая |
| ± 0, 5 - ± 0, 7 | Умеренная |
| ± 0, 7 - ± 1, 0 | Сильная |
Предварительная характеристика направления и тесноты связи между признаками может быть произведена с помощью непараметрических показателей связи: коэффициента Фехнера, коэффициентов корреляции рангов (Спирмена, Кендалла), коэффициента конкордации.
Коэффициент Фехнера Кф оценивает направление и тесноту связи на основе сравнения знаков отклонений значений результативного у и факторного х признаков от их средних арифметических: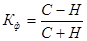 
где С — число совпадений знаков отклонений у от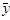 
и х от 
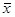по всем единицам изучаемой совокупности; Н — число случаев несовпадений знаков отклонений.
Совпадение знаков отклонений по обоим признакам означает согласованную вариацию, несовпадение — нарушение согласованной изменчивости. Коэффициент Фехнера изменяется от —1 до +1. При Кф = +1 имеет место согласованная изменчивость, при Кф = —1 — обратная изменчивость, при Кф = 0 — согласованная изменчивость отсутствует. Этот коэффициент улавливает направление вариации, но не учитывает ее величину.
Рассчитаем коэффициент Фехнера для рассматриваемого примера. Сравним уровни заработной платы и производительности труда по всем работникам с их средними значениями: 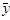= 41280/24 = 1720 руб./чел., 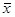= 69600/24 = = 2900 руб./чел. Подсчитаем совпадение знаков отклонений по обоим признакам (табл. 2).
Взаимосвязь уровней производительности труда и заработной платы почтовых работников и расчетные величины для оценки тесноты связи между ними Таблица 2
| Номер работ-ника | Производит. труда х, руб. чел. | Заработная плата у, руб.чел. | Знак отклонения от среднего уровня | Совпадения (несовпадение) знаков | Ранги | Разность рангов d | d2 | ||
| 
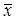
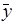
| Rx | Ry | ||||||
| - | - | C | -1 | ||||||
| - | - | C | |||||||
| - | - | C | |||||||
| - | - | C | -1 | ||||||
| - | - | C | -4 | ||||||
| - | - | C | |||||||
| - | - | C | |||||||
| - | - | C | 8, 5 | 2, 5 | 6, 25 | ||||
| - | - | C | 8, 5 | 0, 5 | 0, 25 | ||||
| - | - | C | |||||||
| - | - | C | |||||||
| - | + | Н | |||||||
| + | - | Н | |||||||
| + | + | С | |||||||
| + | + | С | -1 | ||||||
| + | - | Н | 16, 5 | 3, 5 | 12, 25 | ||||
| + | + | С | 16, 5 | -0, 5 | 0, 25 | ||||
| + | + | С | |||||||
| + | + | С | 19, 5 | 4, 5 | 20, 25 | ||||
| + | + | С | 19, 5 | -0, 5 | 0, 25 | ||||
| + | + | С | |||||||
| + | + | С | -1 | ||||||
| + | + | С | |||||||
| + | + | С | |||||||
| Итого | - | - | - | - | - | - | 95, 5 |
Коэффициент Фехнера для нашего примера равен 0, 75[(21-3)/24]. Это дает основание считать, что между производительностью труда работников почтовой связи и их заработной платой существует достаточно тесная прямая связь.
Коэффициент корреляции рангов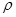 
(коэффициент Спирмена) учитывает согласованность рангов, т.е. номеров или мест, которые занимают единицы совокупности по каждому из анализируемых признаков, и рассчитывается по формуле:
,
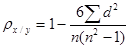где п — количество единиц совокупности; d — разность рангов по признакам х и у.
Порядок сопоставления рангов факторного и результативного показателей таков: единицы совокупности ранжируются по факторному и результативному признакам и каждой единице присваивается номер (место) в упорядоченном ряду признаков. Если встречаются в ряду одинаковые варианты по результативному и факторному признакам, то каждой из них присваивается среднее арифметическое значение их рангов. Коэффициент корреляции рангов может принимать значения от —1 до+1. Значение 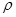= +1 означает строгое изменение рангов в одном направлении, 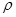= — 1 — в противоположном, при 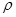= 0 связь отсутствует.
В рассматриваемом примере работники почтовой связи ранжированы по возрастанию факторного признака — уровню производительности труда с 1-го по 24-й номер. При ранжировании почтовых работников трижды встретились одинаковые варианты: х = 2550 у работников, занимающих 8-е и 9-е места, х = 3170 у работников, занимающих 16-е и 17-е места, и х = 3600 у работников, занимающих 19-е и 20-е места по возрастанию производительности труда, поэтому им присвоены средние ранги: 8, 5; 16, 5 и 19, 5.
Коэффициент корреляции рангов составил =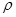 
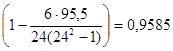, что подтверждает ранее полученный вывод о положительной тесной связи между признаками.
Достоинством непараметрических показателей связи является возможность их использования при анализе взаимосвязи социально-экономических явлений, не имеющих количественного выражения (атрибутивных признаков, например, зависимости заработной платы от уровня образования; от формы собственности предприятия - государственной, частной, кооперативной.
М. Кендэл предложил еще одну меру связи между переменными х и у — коэффициент корреляции рангов Кендэла (т):
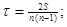S=P+Q
Для вычисления т надо упорядочить ряд рангов переменной х, приведя его к ряду натуральных чисел. Затем рассматривают последовательность рангов переменной у (табл. 7. 6).
Для нахождения суммы S (формула 7.10) находят два слагаемых Р и (). При определении слагаемого Р нужно установить, сколько чисел, находящихся справа от каждого из элементов последовательности рангов переменной у, имеют величину ранга, превышающую ранг рассматриваемого элемента.
| Ранг депутатов по экспертной оценке (х) | ||||||||||
| Ранг депутатов по результатам выборов (у) |
Так, например, первому значению в последовательности рангов переменной у, т.е. числу 2, соответствует восемь чисел (7, 6, 3, 4, 5, 9, 10, 8), которые превышают ранг 2; второму значению соответствует также восемь чисел (7, б, 3, 4, 5, 9, 10, 8), превышающих 1, и т.д. Суммируя полученные таким образом числа, мы получим слагаемое Р, которое можно рассматривать как меру соответствия последовательности рангов переменной у последовательности рангов переменной х. Для нашего примера Р= 35; (8 + 8 + 3 + 3 + 5 + 4 + 3 + 1).
Второе слагаемое Q характеризует степень несоответствия последовательности рангов переменной у последовательности рангов переменной х. Чтобы определить Q, подсчитаем, сколько чисел, находящихся справа от каждого из членов последовательности рангов переменной у, имеет ранг меньше, чем эта единица. Такие величины берутся со знаком «минус».
В рассматриваемом примере Q = -10; (-1-0-4-3-0-0-0-1-1). Следовательно, S = Р + Q = 35 - 10 = 25.
Коэффициент корреляции рангов Кендэла в нашем примере равен:
t = (2 *25)/(10 * 9) = 0, 556.
Коэффициент Кендэла также изменяется в пределах от -1 до +1 и равен нулю при отсутствии связи между рядами рангов.
Для определения тесноты связи между произвольным числом признаков применяют множественный коэффициент ранговой корреляции (коэффициент конкордации):
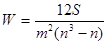, где