
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многофакторный корреляционно-регрессионный анализ
|
|
Задача многофакторного корреляционно-регрессионного анализа заключается:
В изучении факторов, которые оказывают влияние на исследуемый показатель и отборе наиболее значимых;
В определении степени влияния каждого фактора на результативный признак путем построения модели — уравнения множественной регрессии. Уравнение множественной регрессии позволяет установить, в каком направлении и на какую величину изменится результативный показатель при изменении каждого фактора входящего в модель;
В количественной оценке тесноты связи между результативным признаком и факторными.
Математически задача состоит в нахождении функции 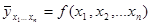
От правильного выбора функции регрессии зависят результаты теоретического анализа и возможность их применения на практике.
Построение моделей множественной регрессии включает следующие этапы:
Выбор формы связи (уравнения регрессии) путем перебора нескольких аналитических функций;
Отбор значимых факторных признаков (опирается на сравнение частных коэффициентов эластичности, b-коэффициентов, D-частных коэффициентов детерминации);
Обеспечение достаточного объема совокупности для получения несмещенных оценок (их количество должно быть в несколько раз больше, чем число факторов, включаемых в модель. На каждый фактор должно приходиться, как минимум, 5-6 наблюдений.
Сложность выбора функции состоит в том, что результативный признак с разными факторами может находиться в различных формах связи— прямолинейных и криволинейных. Эмпирическое обоснование типа функции с помощью графиков парных связей практически непригодно для множественной корреляции и регрессии.
Выбор формы уравнения множественной регрессии основывается на теоретическом анализе изучаемого явления.
Практика многофакторного регрессионного анализа социально-экономических явлений показывает, что для описания их взаимосвязей можно использовать пять типов моделей:
линейная 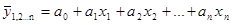
степенная 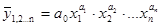
показательная 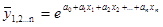
параболическая 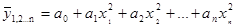
гиперболическая 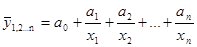
Чаще всего останавливаются на линейных моделях. Это объясняется тем, что параметры линейных уравнений легко интерпретируются, а сами модели просты и удобны для экономического анализа.
Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена используя сравнительный анализ частных коэффициентов эластичности Эi, b-коэффициентов и частных коэффициентов детерминации Di.
Рассмотрим принципы анализа степени влияния факторов на примере, когда в уравнение регрессии были включены пять факторов (табл. 1).
Если сопоставить значения коэффициентов эластичности (графы 2 и 5 табл. 1), то можно видеть, что главным фактором изменения результативного показателя является фактор х5; при его изменении на 1% у возрастает на 79, 5%. Вторым по силе влияния на результативный показатель является фактор х1 и т.д. (графа 5).
Сравнение значений bj позволяет сделать вывод, что наибольший вклад в изменение результативного признака вносят факторы х5, х4 и х1 (графа 6 табл. 1)
Сопоставление значений коэффициентов Dj, позволяет сделать вывод, что наибольшую долю влияния имеет фактор х5: роль этого фактора в вариации результативного показателя составляет 52, 5% общего влияния пяти факторов на результативный показатель. Доля влияния других факторов значительно уступает доле влияния фактора х5. Следовательно, наибольшие возможности в изменении результативного показателя связаны с изменением фактора х5, затем х1 и далее х4..
Таблица 1
| Факторы | Значения коэффициентов | Ранг факторов по величине коэффициентов | Средний ранг | ||||
| Эj | bj | Dj | Эj | bj | Dj | ||
| X1 | 0, 173 | 0, 204 | 0, 162 | ||||
| X2 | 0, 133 | 0, 114 | 0, 076 | ||||
| X3 | 0, 108 | 0, 144 | 0, 104 | ||||
| X4 | 0, 158 | 0, 253 | 0., 133 | ||||
| X5 | 0, 795 | 0, 732 | 0, 525 |
Также часто используется метод пошаговой регрессии, состоящий в последовательном включении факторов в модель и оценке их значимости. Факторы поочередно вводятся в уравнение. При введении фактора определяется, насколько увеличивается величина множественного коэффициента корреляции R. Если при включении в модель фактора xiвеличина R увеличивается, а коэффициент регрессии аi не изменяется или меняется незначительно, то данный фактор существенен и его включение в модель необходимо. Одновременно используется и обратный метод, т.е. исключение факторов, ставших незначимыми на основе t-критерия Стьюдента.
Наличие между двумя факторами весьма тесной линейной связи (линейный коэффициент корреляции г превышает по абсолютной величине 0, 85) называется коллинеарностью, а между несколькими факторами — мультиколлинеарностью.
Причины возникновения мультиколлинеарности между признаками состоят, во-первых, в том, что анализируемые признаки характеризуют одну и ту же сторону явления или процесса (например, уставной фонд и численность работников характеризуют размер предприятия) и включать их в модель одновременно не целесообразно; во-вторых, факторные признаки являются составными элементами друг друга, дублируют друг друга или их суммарное значение дает постоянную величину (например, энерговооруженность и фондовооруженность, удельный вес заемных и собственных средств).
Если в модель включены мультиколлинеарные факторы, то уравнение регрессии будет неадекватно отражать реальные взаимосвязи, будут искажены величины параметров модели (завышены) и затруднена экономическая интерпретация коэффициентов регрессии и корреляции.
Поэтому при построении модели исключают один из коллинеарных факторов исходя из качественного и логического анализа.
В уравнении множественной регрессии в линейной форме параметры а1, а2, аз,..., аn — коэффициенты регрессии, показывают степень влияния соответствующих факторов на результативный признак при закреплении остальных факторов на среднем уровне, т.е. насколько изменится у при увеличении соответствующего фактора xi на 1 пункт его единицы изменения;
параметр а0 — свободный член, экономического смысла не имеет.
Параметры уравнения множественной регрессии, как и парной, рассчитываются методом наименьших квадратов на основе решения системы нормальных уравнений. Для линейного уравнения регрессии с п факторами строится система из (n+1) нормальных уравнений:
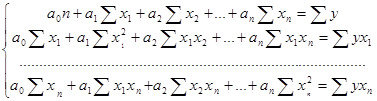
Поскольку коэффициенты регрессии между собой несопоставимы (факторы имеют разные единицы измерения), то нельзя сравнивать силу влияния каждого фактора на результативный признак на основании коэффициентов регрессии.