
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Можно также использовать опыт предыдущих исследований, и там, где выбранные формы уравнений связи давали удовлетворительный результат, рекомендовать их использовать в дальнейшем.
|
|
Наиболее часто для характеристики связей экономических показателей используют следующие типы функций:

|
В нашем примере (зависимости числа туристов от затрат фирмы на рекламу) эмпирическая линия регрессии все же больше всего приближается к прямой и, следовательно, теоретическая линия регрессии может быть представлена уравнением вида:
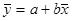
Для нахождения параметров а и b уравнения регрессии используем метод наименьших квадратов. При применении метода наименьших квадратов, считается, что сумма квадратов отклонений эмпирических точек теоретической линии регрессии должна быть величиной минимальной:
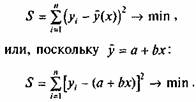
|
Следовательно, применение метода наименьших квадратов для определения параметров а и bпрямой, наиболее соответствующей эмпирическим данным, сводится к задаче на экстремум.
Функция двух переменных S(а, b) может достигнуть экстремума в том случае, когда первые частные производные этой функции равняются нулю, т.е. когда:
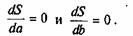
|
Вычисляя эти частные производные, получим
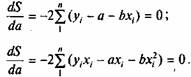
|
После несложных преобразований получим систему нормальных уравнений способа наименьших квадратов для определения величины параметров а и b уравнения прямолинейной корреляционной связи по эмпирическим данным:
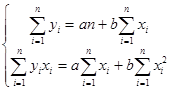 (2) (2)
|
Решая систему уравнений (2) относительно a и b, получим следующие формулы для определения этих параметров:
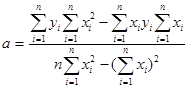 =(19050*2013-192310*199)/20*2013-1992=77960/659=118, 3
=(19050*2013-192310*199)/20*2013-1992=77960/659=118, 3
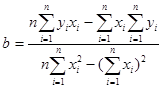 =20*192310-199*19050/659=55250/659=83, 84
=20*192310-199*19050/659=55250/659=83, 84
Для определения коэффициентов a и b составим вспомогательную таблицу 5
Получим систему уравнений
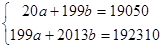
Таблица 5
| № п/п | Затраты на рекламу (усл. ден. ед.) х | Кол-во туристов, воспользовавшихся услугами фирмы, чел. У | x*y | x^2 | y регрессии | y регрессии по корреляционной таблице | у2 |
| 789, 02 | 803, 08 | ||||||
| 789, 02 | 803, 08 | ||||||
| 789, 02 | 803, 08 | ||||||
| 872, 86 | 873, 14 | ||||||
| 872, 86 | 873, 14 | ||||||
| 872, 86 | 873, 14 | ||||||
| 872, 86 | 873, 14 | ||||||
| 872, 86 | 873, 14 | ||||||
| 956, 7 | 943, 2 | ||||||
| 956, 7 | 943, 2 | ||||||
| 956, 7 | 943, 2 | ||||||
| 956, 7 | 943, 2 | ||||||
| 956, 7 | 943, 2 | ||||||
| 1040, 54 | 1013, 26 | ||||||
| 1040, 54 | 1013, 26 | ||||||
| 1040, 54 | 1013, 26 | ||||||
| 1040, 54 | 1013, 26 | ||||||
| 1124, 38 | 1083, 32 | ||||||
| 1124, 38 | 1083, 32 | ||||||
| 1124, 38 | 1083, 32 | ||||||
| Итого 20 | 19050, 16 | 18793, 94 |
В результате: а = 118, 3; b= 83, 84 и  = 118, 3+ 83, 84x.
= 118, 3+ 83, 84x.
Параметр a – это свободный член уравнений регрессии, он определяет положение начальной точки линии регрессии в системе координат при х=0 y=а
Параметр b называется коэффициентом регрессии, является угловым коэффициентом линии регрессии и показывает, насколько изменяется в абсолютном значении результативный признак при изменении на единицу признака фактора х.
Если данные сгруппированы (например, представлены в виде корреляционной таблицы 4), то система нормальных уравнений имеет вид
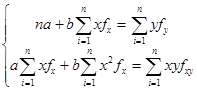
|
где fx— частота повторения данного варианта значения у;
fy — частота повторения данного варианта значения х;
fxy — частота повторения данного сочетания значений х и у.
Для нашего примера имеем:
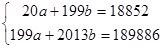
Выражаем из первого уравнения системы показатель a, подставляем во второе уравнение системы
а=942, 6-9, 95b; 199*(942, 6-9, 95b)+2013b=189886; b=2308, 6/32, 95=70, 06;
а=942, 6-9, 95*70, 06=245, 5 и получаем
a=245, 5; b=70, 06
Уравнение регрессии будет иметь вид:  = 242, 6 + 70, 06x
= 242, 6 + 70, 06x
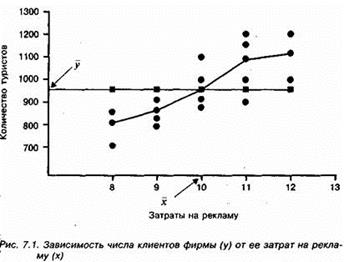
Графическое изображение эмпирической и теоретической линии связи представлено на рис. 1.
|
Для нахождения параметров гиперболы 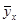 =а+b/х по способу наименьших квадратов пользуются аналогичной прямолинейной зависимости системой нормальных уравнений, в которой х заменен на 1/х.
=а+b/х по способу наименьших квадратов пользуются аналогичной прямолинейной зависимости системой нормальных уравнений, в которой х заменен на 1/х.
Для определения параметров параболы второго порядка 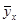 =а+bх+сх2 в соответствии метода наименьших квадратов решается система, состоящая из трех нормальных уравнений:
=а+bх+сх2 в соответствии метода наименьших квадратов решается система, состоящая из трех нормальных уравнений:
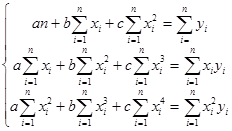
Выбор теоретической формы корреляционной связи всегда несколько условен, так как в действительности зависимости между признаками лишь приблизительно соответствуют функциональным. Поэтому только при высокой тесноте связи между признаками линия регрессии имеет содержательный смысл и практическое значение.