
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические сведения. Имитация представляет собой численный метод проведения на ЭВМ экспериментов с математическими моделями
|
|
Имитация представляет собой численный метод проведения на ЭВМ экспериментов с математическими моделями, описывающими поведение сложной системы в течение заданного или формируемого периода времени. Поведение компонентов сложной системы и их взаимодействие в имитационной модели чаще всего описывается набором алгоритмов, реализуемых на некотором языке моделирования.
Термин «имитационная модель» используют в том случае, когда речь идет о проведении численных расчетов и в частности о получении статистической выборки на математической модели, например, для оценки вероятностных характеристик некоторых выходных параметров.
Имитационное моделирование применяется для проведения расчетов характеристик будущей системы. Наиболее важным для исследователя является показатель эффективности системы. Имитируя различные реальные ситуации на модели, исследователь получает возможность решения таких задач как оценка эффективности тех или иных принципов управления системой, сравнение вариантов структурных схем, определение степени влияния изменений параметров системы и начальных условий на показатель эффективности системы. Примерами расчетов на имитационных моделях также могут служить вычисления характеристик производительности, надежности, качества функционирования и т.п., которые необходимо определить как функции внутренних и внешних параметров системы.
Вероятностный характер процессов, происходящих в сложных системах, приводит к невозможности аппроксимации явлений функциональными зависимостями. Доминирующим методом при моделировании сложных систем является способ алгоритмического описания происходящих в системе процессов.
Системы массового обслуживания (СМО) предназначены для многократного проведения некоторой однотипной элементарной операции, которую называют операцией обслуживания.
Операции обслуживания, для осуществления которых создается СМО, проводятся в связи с тем, что имеется массовый спрос на определенный вид обслуживания. В свою очередь, массовый спрос осуществляется через множество индивидуальных требований или заявок.
Предмет теории массового обслуживания - установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью обслуживания.
Множество моментов поступления в систему требований называется входящим потоком данной СМО. Интенсивность потока  - среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной, так и переменной.
- среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной, так и переменной.
Поток событий называется простейшим (стационарным, пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не обладает последействием.
Для простейшего потока с интенсивностью  интервал Т между соседними событиями имеет показательное распределение с плотностью
интервал Т между соседними событиями имеет показательное распределение с плотностью
 (
( )
)
Для этого закона математическое ожидание и среднеквадратичное отклонение равны  .
.
Для СМО, описывающих функционирование различных реальных объектов, характерно то, что они работают под воздействием случайных факторов. Моменты поступления требований являются случайными величинами, длительности обслуживания — тоже случайные величины. Поэтому процесс функционирования СМО носит случайный характер. В связи с этим обстоятельством методы исследования СМО сводятся к построению некоторого случайного процесса, описывающего эволюцию системы, и исследованию этого процесса.
В данной лабораторной работе производится имитация работы роботизированного участка станков на базе теории массового обслуживания. Предполагается, что станки работают параллельно, роботом оснащен каждый станок или один робот на два станка. Задаем следующие исходные параметры:
1) время обработки (время работы станка)  ;
;
2) число станков 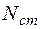 ;
;
3) число роботов 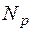 ;
;
4) время работы робота 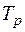 .
.
Заготовки детали поступают на обработку через интервал времени  (i =1, n), который является случайной величиной с известным математическим ожиданием. Величины
(i =1, n), который является случайной величиной с известным математическим ожиданием. Величины  и
и 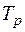 также являются случайными с известными мат. ожиданиями. Работа организована следующим образом: заготовка поступает на обработку на любой свободный станок, оснащенный роботом. Робот в течение времени
также являются случайными с известными мат. ожиданиями. Работа организована следующим образом: заготовка поступает на обработку на любой свободный станок, оснащенный роботом. Робот в течение времени 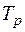 перемещает, устанавливает заготовку в зоне обработки, далее идет обработка длительностью
перемещает, устанавливает заготовку в зоне обработки, далее идет обработка длительностью  , затем снова в работу включается робот, манипулируя заготовкой в течение того же времени
, затем снова в работу включается робот, манипулируя заготовкой в течение того же времени 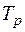 .
.
Диаграмма, показывающая схему работы на примере двух станков, оснащенных роботами, показана на рис. 2. Из анализа этой диаграммы можно определить загрузку обоих станков, роботов. Если количество станков большое, то графически решить задачу затруднительно.
Если имитировать работу роботизированного участка, приняв случайный характер величин  ,
,  и
и 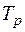 , задав
, задав 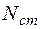 и
и 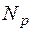 , то можно определить по результатам расчета программы важные для нас величины: коэффициенты загрузки станков и роботов.
, то можно определить по результатам расчета программы важные для нас величины: коэффициенты загрузки станков и роботов.
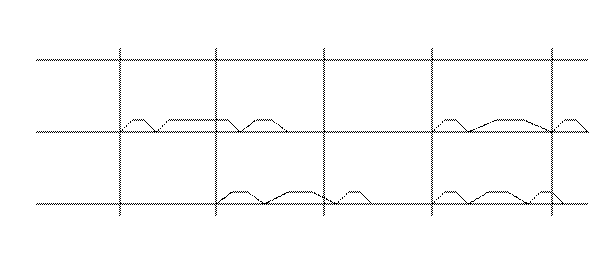
Рис. 2. Диаграмма работы двух станков,
оснащенных роботами