
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Точечные оценки измеряемой величины. Оценка среднего значения измеряемой величины.
|
|
Оценку неизвестного параметра генеральной совокупности случайной величины одним числом называют точечной оценкой. Отклик оценивается по результатам прямых или косвенных измерений. Способ оценки зависит от природы отклика (случайная или неслучайная величина) и точности измерений.
1) Отклик является неслучайной величиной. Ошибки измерения малы по сравнению со значениями отклика.
При i -ом измерении получим: 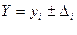 , где Y – истинное значение измеряемой величины (отклика);
, где Y – истинное значение измеряемой величины (отклика); 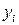 – измеренное значение отклика;
– измеренное значение отклика; 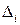 – погрешность измерения.
– погрешность измерения.
Если 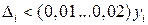 , то погрешностью измерения можно пренебречь и полученное после первого измерения значение
, то погрешностью измерения можно пренебречь и полученное после первого измерения значение 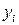 принять за истинное.
принять за истинное.
2) Отклик является неслучайной величиной, но погрешностью измерения пренебречь нельзя.
Если все n измерений величины а проведены с одинаковой точностью, то такие измерения называют равноточными измерениями.
При равноточных измерениях в качестве оценки истинного значения величины y используют среднее арифметическое значение результатов измерений.
Среднее арифметическое значение величины y:
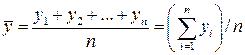 (3.2)
(3.2)
При расчете величины дисперсии по результатам экспериментальных измерений следует руководствоваться следующими правилами.
Вариант 1. Измерение известной величины а (эталона).
В качестве эффективной оценки дисперсии используют средний квадрат отклонения результатов измерений  от значения а.
от значения а.
 (3.3)
(3.3)
Вариант 2. Измерение неизвестной величины.
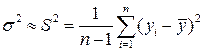 , (3.3”)
, (3.3”)
Сомножитель  – гарантирует несмещенность оценки.
– гарантирует несмещенность оценки.
Среднее квадратическое отклонение величины 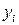 от среднего значения
от среднего значения 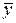 :
:
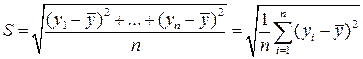 ; (3.4)
; (3.4)
Величина стандартного отклонения в квадрате: 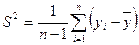 называется эмпирической дисперсией.
называется эмпирической дисперсией.
Точность соответствия 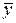 и
и 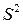 истинному значению тем выше, чем больше число измерений n.
истинному значению тем выше, чем больше число измерений n.
Рассмотренные оценки являются несмещенными и состоятельными. Если случайные ошибки измерения строго подчиняются нормальному закону распределения вероятностей, то оценки будет эффективными. При неограниченном числе измерений оценки также становятся эффективными.
3) При оценке неравноточных измерений.
В этом случае при обработке результатов экспериментальных измерений используют веса измерений – числа 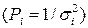 обратнопропорциональные дисперсиям ошибок измерений.
обратнопропорциональные дисперсиям ошибок измерений.
Взвешенное среднее арифметическое значение:
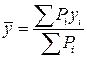 (3.5)
(3.5)
Взвешенное среднее квадратическое отклонение:
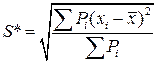 (3.6)
(3.6)
Эта оценка несмещенная и состоятельная. При дополнительном предположении, что случайные ошибки измерения подчиняются нормальному закону распределения вероятностей, оценка является эффективной.
Вес измерения – это некоторое число, характеризующее мощность (или значимость) измерения. Чем больше вес i -ого измерения, тем в большей степени данное измерение соответствует истинному значению а измеряемой величины в статистическом смысле. Вес измерения пропорционален числу измерений и обратно пропорционален дисперсии среднего значения результатов измерений (дисперсии средних значений обратно пропорциональны количествам измерений).
Однако, при оценках измеряемых величин важна не величина весов, а их отношение друг к другу, т.е., как правило, задают 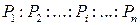 . Где Pi можно задать одним из следующих способов: а)
. Где Pi можно задать одним из следующих способов: а) 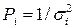 ; б)
; б) 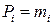 (чем больше объем измерений в серии, тем выше надежность средних); в) при использовании приближенных значений дисперсий
(чем больше объем измерений в серии, тем выше надежность средних); в) при использовании приближенных значений дисперсий 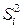 в качестве веса принимают величину
в качестве веса принимают величину 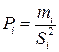 .
.