Визначення довірчого інтервалу для оцінки маточікування у генеральної сукупності з довільним розподілом випадкових величин на основі середнього арифметичного великої вибірки

Щоб визначити довірчий інтервал для невідомого значення параметра m, потрібно знати розподіл випадкових величин у генеральній сукупності. Для того, щоб знайти закон розподілу випадкових величин у генеральній сукупності, слід дослідити розподіл випадкових величин у вибірці і на основі цього сформулювати статистичну гіпотезу про закон розподілу генеральної сукупності.

Однак виявляється, що не обов’язково вживати відомі методи отримання інформації про статистичний розподіл генеральної сукупності, якщо оцінюємо матсподівання. Існує більш простий спосіб, що базується на використанні центральної теореми теорії імовірності. Як відомо, при певних умовах, що виконуються у загальному випадку, довільний статистичний розподіл середнього арифметичного випадкових величин у вибірці прямує до нормального, коли кількість випадкових величин необмежено зростає. Це означає, що розподіл середнього арифметичного з вибірки, що відбирається з генеральної сукупності з довільним розподілом, мало чим відрізняється від нормального розподілу, якщо об’єм (розмірність) вибірки є достатньо великим. У практиці приймають, що розподіл середнього арифметичного з вибірки можна замінити нормальним розподілом, якщо об’єм вибірки n> 30 (великі вибірки).

Отже, якщо використовуємо велику вибірку, можемо оцінювати матсподівання генеральної сукупності, не знаючи навіть закону розподілу випадкових величин у цій сукупності.

Приклад.

1. Відбираємо вибірку об’ємом n =100 елементів і обчислюємо середнє арифметичне вибірки. Припустимо, що воно становить 120.

2. Обчислюємо стандартне відхилення вибірки згідно виразу

.

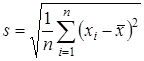Припустимо, що стандартне відхилення s вибірки становить 21. У такому разі приймаємо, що .

3. Визначивши значення стандартного відхилення з генеральної сукупності, визначаємо

.

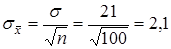4. Знаходимо у таблицях нормального розподілу значення t, що відповідає вибраній довірчій імовірності .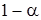

5. Обчислені і відомі значення i (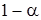 ) вставляємо до виразу

.
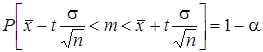