при цьому k означає кількість степенів свободи.

Розподіл (3.3) відомий у статистиці як розподіл Стьюдента. Він є симетричним і своїм виглядом нагадує нормальний. Коли k ³ 30, розподіл Стьюдента практично збігається з нормальним.

Приклад 1. Випадкові величини X генеральної сукупності описуються нормальним розподілом. З цієї сукупності відібрано вибірку, об’єм якої становить n = 10 елементів. На основі даних з вибірки потрібно оцінити матсподівання m генеральної сукупності, тобто визначити довірчий інтервал для m.

Обчислюємо середнє арифметичне і стандартне відхилення вибірки. Припустимо, що 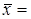24, a s = 2, 7. Задамо довірчу імовірність x. Нехай 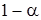= 0, 98. У такому разі (див. рис. 3.1)

.

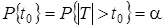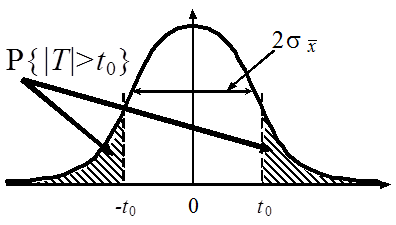
Rys. 1.

З таблиці для розподілу Стьюдента шукаємо t для a = 0, 02 i k = 10 – 1 = 9. Маємо t = 2, 821» 2, 8. Тому

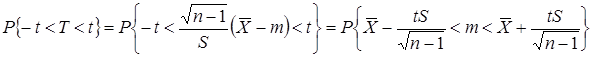.(3.3)

Оскільки 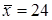, s = 2, 7, t = 2, 8, то шуканий довірчий інтервал буде таким:

,

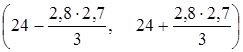А після виконання арифметичних операцій маємо (21, 48, 26, 52).