Подъемной силы крыла

Коэффициент аэродинамической подъемной силы крыла 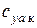зави­сит от геометрических и аэродинамических характеристик профиля, геометрических параметров крыла, угла атаки α, критериев подобия Re и M. Рассмотрим методику определения 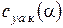для изолированного крыла с учетом вышеперечисленных параметров.

Зависимость коэффициента подъемной силы 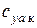от угла атаки в общем случае можно поде­лить на две области. Первая область 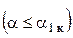характеризуется безотрыв­ным обтеканием и линейной зависимостью 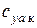от (коэффициент подъемной силы прямо пропорционален углу атаки). Вторая область характеризуется тем, что по мере увеличения угла атаки (при 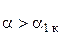) и расширении области отрыва потока (это так называемый диффузорный отрыв потока) рост коэффициента подъемной силы замедляется и достигает максимума при критическом угле атаки крыла, а затем уменьшается. Здесь 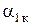- угол атаки крыла, при котором начинается интенсивный срыв потока и который называется допустимым углом атаки или углом тряски. Угол атаки, соответствующий 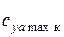, называется критическим углом атаки 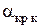. Отметим, что в данной работе угол 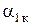определяется из условия гладкого сопряжения линейной и нелинейной областей кривой 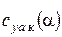. Характер зависимости нелинейной части от угла атаки для упрощения выбран в виде квадратичного полинома, что не всегда соответствует действительности. В следствие этого, значения угла 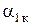могут оказаться заниженными, особенно для больших чисел Маха.

3.1. Расчет производной коэффициента подъемной силы по углу атаки 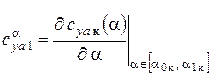(на линейном участке) для числа Рейнольдса производится по формулам [3]:

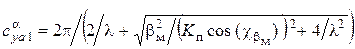, (1)

где

, , .

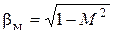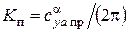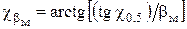3.2. Расчет нулевого угла атаки крыла 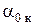. С учетом крутки крыла угол 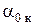определяется из следующих выражений [4]:

,

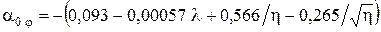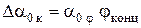, (2)

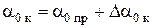. (3)

Здесь 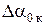- слагаемое, зависящее от крутки крыла, которое определено для случая равномерной крутки по размаху крыла. С точки зрения получения максимального аэродинамического качества K рекомендуется угол крутки концевого сечения взять 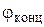» - 4° (если 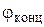< 0, то аэродинамический угол атаки концевого сечения меньше корневого).

3.3. Расчет критического угла атаки крыла :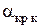

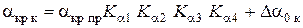, (4)

где

;

;

;

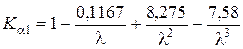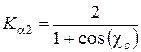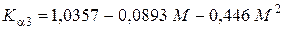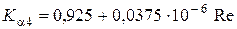, если ;

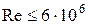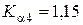при .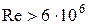

3.4. Расчет максимального значения коэффициента подъемной силы 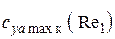крыла (для числа Рейнольдса Re₁) с учетом сжимаемости можно приближенно определить по формулам:

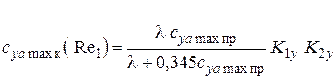, (5)

где

,

.

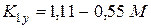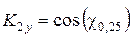3.5. Расчет угла окончания линейного участка 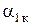из условия гладкого сопряжения линейного и нелинейного участка:

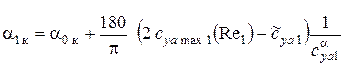, град, (6)

где

.

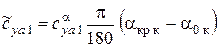3.6. Расчет коэффициента подъемной силы 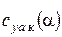(на линейном и нелинейном участках).

Предварительно определяем коэффициент 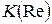, учитывающий влияние числа Рейнольдса на коэффициент подъемной силы [3, 5]. Расчет производится после определения параметра t с помощью выражения

,

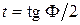где F - угол схода (угол между верхней и нижней поверхностями) хвостовой кромки профиля. Приближенное значение F можно вычислить по формуле

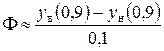в радианах.

Здесь 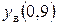и 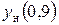- координаты верхней и нижней поверхностей профиля при 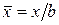= 0, 9.

Для четырех – и пятизначных профилей NACA можно использовать более простую формулу:

.

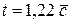Коэффициент, 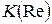можно рассчитать по формуле

,

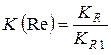где ,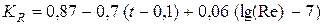

.

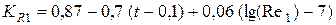Здесь принято, что переход ламинарного к турбулентному режиму течения в пограничном слое происходит около передней кромки [3]. Формулу для 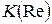можно использовать в диапазоне чисел Рейнольдса 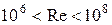. При ориентировочных расчетах можно полагать .

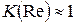Коэффициент подъемной силы крыла на линейном участке (для числа Рейнольдса Re₁) определяется выражением

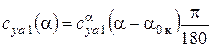, (7)

где углы 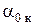, a измеряются в градусах.

Определим теперь 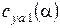на нелинейном участке при 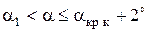(для числа Рейнольдса Re₁). При диффузорном отрыве потока можно принять [5]:

,

,

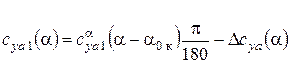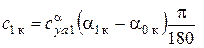где .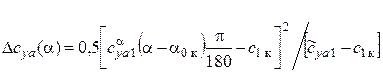

С учетом влияния числа Рейнольдса окончательно получим выражение для зависимости коэффициента подъемной силы 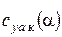крыла для данного угла атаки a

;

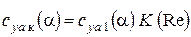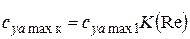
и выражение для производной коэффициента подъемной силы

.
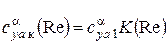