Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекції 2-5.
|
|
Загальні принципи побудови економетричних моделей.
Моделі парної регресії
План
| 1. | Регресійний аналіз та його особливості |
| 2. | Діаграма розсіювання регресійної функції |
| 3. | Модель парної лінійної регресії |
| 4. | Методи знаходження оцінок параметрів економетричної моделі з двома змінними |
| 5. | Загальна, пояснююча та непояснююча дисперсії. Коефіцієнти кореляції та детермінації |
| 6. | Умови Гауса-Маркова для випадкової змінної |
| 7. | Властивості оцінок параметрів моделі парної регресії |
| 8. | Побудова довірчих інтервалів |
| 9. | Перевірка нульових гіпотез |
| 10. | Адекватність економетричної моделі |
1. Регресійний аналіз та його особливості
Під регресією розуміють односторонню стохастичну залежність однієї випадкової змінної від другої чи декількох інших випадкових змінних. Таким чином, регресія встановлює відповідність між випадковими змінними. Наприклад, при визначенні залежності обсягу податкових надходжень (y) від ставки податку (х) мова йде про визначення одностороннього зв’язку, тобто про регресію. Обидві змінні є випадковими. Кожному значенню х відповідає множина значень у і навпаки, кожному значенню у відповідає множина значень х. Таким чином, ми маємо справу із статистичним розподілом значень х та у. Виходячи з цих розподілів, ми повинні знайти стохастичну залежність між у та х. Одностороння стохастична залежність виражається за допомогою функції, яка на відміну від строгої математичної залежності називається функцією регресії чи просто регресією.
Принциповою різницею між строгою функціональною залежністю та функцією регресії є те, що у першому випадку аргумент (незалежна змінна) повністю визначає значення функції, і для неї існує обернена (наприклад, функція у = х 2, тоді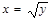 
). Функція регресії цією властивістю не володіє. Отже, якщо між явищами відсутній функціональний зв’язок, а має місце тільки стохастичний, то функція регресії буде незворотною.
За числом змінних, введених у регресійне рівняння, розрізняють просту (парну) та множинну (багатофакторну) регресії. Відносно форми залежності моделі діляться на лінійну та нелінійну регресії.
При побудові регресійної функції спочатку потрібно провести ідентифікацію змінних, тобто визначити, яка із них є ознакою (залежною чи поянюваною змінною), а які є незалежними (факторами чи пояснюючими змінними). Якщо в загальному випадку рівняння регресії для двох змінних записати y=f(x), то y – пояснювана змінна, а х – пояснююча. Потім потрібно провести специфікацію моделі, тобто встановити форму зв’язку між змінними.