
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Економетричної моделі з двома змінними
|
|
а) Метод найменших квадратів (МНК) за системою нормальних рівнянь. Цей метод є найточнішим методом знаходження оцінок параметрів економетричної моделі. Провівши економічний аналіз певного процесу з врахуванням характеру хмарки точок на діаграмі розсіювання, переходимо до вирівнювання дослідних даних, яке полягає у побудові гіпотетичної лінії. Основною вимогою при цьому є зведення до мінімуму помилок специфікації форм зв’язку між змінними. Ці помилки визначаються через відхилення емпіричних даних уі від значень регресії  , тобто вони формують значення збуреної змінної е:
, тобто вони формують значення збуреної змінної е:
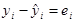
З графіка (рис. 1.4) бачимо, що еі – відхилення дослідної точки від оціночної прямої, виміряне по вертикалі. Це відхилення може бути додатнім чи від’ємним в залежності від того, по яку сторону від лінії розміщена конкретна точка.
При виборі прямої можна висунути вимогу, щоб сума відхилень всіх точок від лінії регресії була рівна нулеві, тобто
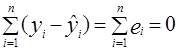 .
.
Ця умова означає, що сума додатних відхилень повинна бути рівною сумі від’ємних. Дотримання даної умови не дає можливості однозначно визначити розміщення вирівнюючої прямої на площині. Дану умову задовольняє нескінчена множина прямих, тобто через задану точку з координатами (хі; уі) проходить пучок прямих.
Для знаходження однозначного розв’язку використовуємо один із показників розсіювання випадкової величини – дисперсію. Якщо всі відхилення піднести до квадрату і просумувати, то результат буде безпосередньо залежати від розкиду точок довкола шуканої лінії. Із множини можливих прямих має бути вибрана така, для якої міра розсіювання дослідних точок буде мінімальною. Це можна представити наступним чином:
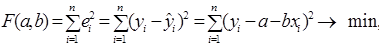 (1.3)
(1.3)
тобто сума квадратів відхилень емпіричних значень змінної у від значень, обчислених за рівнянням прямої, повинна бути мінімальною.
Метод, в основу якого покладена вимога мінімізації суми квадратів відхилень, називається методом найменших квадратів (МНК). З його допомогою знаходять такі оцінки параметрів рівняння регресії, які зводять до мінімуму вибрану міру розсіювання. При цьому проходить вирівнювання емпіричних значень в одну лінію регресії. У випадку лінійного зв’язку між змінними ця лінія є прямою.
Таким чином, проблема визначення прямої регресії зводиться до мінімізації функції (1.3). Необхідною умовою цього є перетворення в нуль перших частинних похідних цієї функції по кожній змінній а та b. Візьмемо ці частинні похідні та прирівняємо їх до нуля:
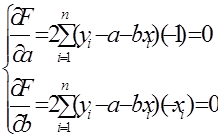
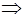
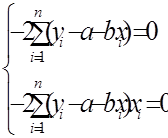
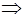
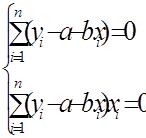
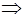

В результаті виконання перетворень отримаємо наступну систему, яка називається системою нормальних рівнянь:
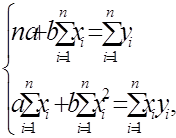 (1.4)
(1.4)
розв’язавши яку, знаходимо a та b:
Розв’язки системи (1.4) методом Крамера можна знайти за формулами:
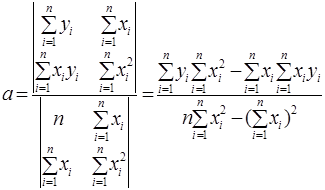 (1.5)
(1.5)
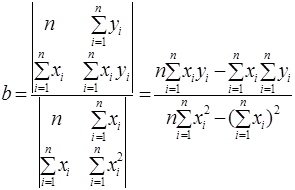 (1.6)
(1.6)
Значення a та b, обчислені за формулами (1.5) і (1.6), є оцінками параметрів α та β регресії, отримані МНК. Маючи значення a та b можна обрахувати значення регресії для заданої області значень пояснюючої змінної х. Ці значення представляють собою найкращу з точки зору МНК лінійну апроксимацію для емпіричних значень уі, оскільки вибрана міра розсіювання – стандартне відхилення зводиться при цьому до мінімуму.
б) МНК через відхилення від середніх. Розглянемо методику оцінювання параметрів з допомогою методу відхилень від середніх арифметичних. Основу даного методу складають властивості оцінок, знайдених МНК, які полягають в тому, що лінія регресії обов’язково проходить через точку середніх значень 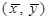 .
.
Поділимо перше рівняння системи (1.4) на n:
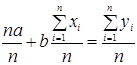 .
.
У результаті отримаємо
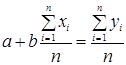 , або
, або
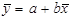 . (1.7)
. (1.7)
Далі віднімемо від розрахункового значення змінної y (1.2) її середнє значення, знайдене за формулою (1.7):
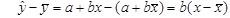 .
.
Звідси 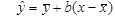 . (1.8) Тоді відхилення фактичних значень змінної y від розрахункових, знайдених по формулі (1.8):
. (1.8) Тоді відхилення фактичних значень змінної y від розрахункових, знайдених по формулі (1.8):
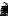 .
.
 та
та 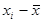 – це відхилення змінних y та x від їх середніх значень. Для простоти позначимо їх
– це відхилення змінних y та x від їх середніх значень. Для простоти позначимо їх 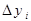 та
та 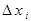 .
.
Дальше розглядаємо функцію, що представляє собою суму квадратів відхилень дійсних значень змінної y від розрахункових і досліджуємо її на min.
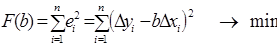
Оскільки отримана функція залежить тільки від b, то знаходимо частинну похідну цієї функції по b і прирівнюємо її до нуля.
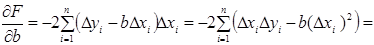
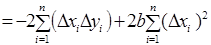 .
.
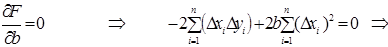
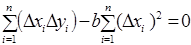
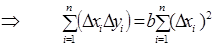 .
.
Звідси знаходимо параметр b:
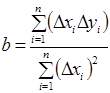 . (1.9)
. (1.9)
Значення оцінки а знайдемо з формули (1.7):
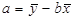 (1.10)
(1.10)
Формули (1.9) та (1.10) – це формули для знаходження оцінок параметрів економетричної моделі методом найменших квадратів через відхилення від середніх.
Формулу (1.9) можна представити в іншому вигляді. Якщо розділити чисельник і знаменник на 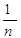 , то отримаємо:
, то отримаємо:
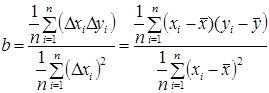 .
.
Ми отримали в чисельнику коефіцієнт коваріації між змінними x та y, який обчислюється за формулою:
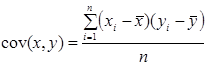 ,
,
а в знаменнику маємо дисперсію змінної x, яка знаходиться за формулою:
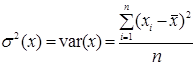 .
.
Тоді формула (1.9) матиме вигляд:
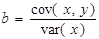 .
.
Приклад 1.1. Для десяти підприємств регіону за умовний деякий період відомі числові значення двох економічних показників: валова продукція y (млн. грн.) і вартість основних виробничих фондів x (млн. грн.), (табл.1.1). Для дослідження характеристики впливу вартості основних виробничих фондів (x) на випуск валової продукції (y) підприємства з допомогою економетричної моделі необхідно:
1. Зробити специфікацію моделі.
2. Знайти оцінки параметрів моделі з допомогою МНК (за системою нормальних рівнянь та через відхилення від середніх).
3. Побудувати оціночну пряму.
Таблиця 1.1
| № підприємства | Валовий випуск продукції, млн.грн., уі | Основні виробничі фонди, млн.грн., хі |
| 2, 2 | 1, 4 | |
| 4, 2 | 2, 2 | |
| 5, 7 | 3, 3 | |
| 6, 8 | 2, 6 | |
| 5, 9 | 3, 2 | |
| 7, 6 | 4, 5 | |
| 9, 5 | 5, 1 | |
| 8, 4 | 6, 7 | |
| 10, 1 | 7, 3 | |
| 12, 3 | 8, 9 |
¨ Розв’язування.
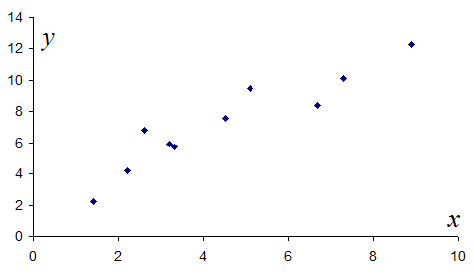 |
1. Побудуємо діаграму розсіювання залежності валового випуску продукції (у) від вартості основних виробничих фондів підприємства (х):
Рис.1.5. Діаграма розсіювання
Розміщення точок на діаграмі розсіювання дає можливість зробити припущення про існування лінійної форми зв’язку у вигляді функції (1.2):
ŷ =а+bх,
де ŷ – розрахунковий обсяг випуску валової продукції, млн. грн.; х – вартість основних виробничих фондів, млн. грн.
2. Для спрощення розрахунків при знаходженні оцінок a та b параметрів економетричної моделі побудуємо таблицю:
| № п/п | yi | xi | xi2 | xi× yi | D xi | (D xi)2 | D yi | D xi × D yi |
| 2, 2 | 1, 4 | 1, 96 | 3, 08 | -3, 12 | 9, 73 | -5, 07 | 15, 82 | |
| 4, 2 | 2, 2 | 4, 84 | 9, 24 | -2, 32 | 5, 38 | -3, 07 | 7, 12 | |
| 5, 7 | 3, 3 | 10, 89 | 18, 81 | -1, 22 | 1, 49 | -1, 57 | 1, 92 | |
| 6, 8 | 2, 6 | 6, 76 | 17, 68 | -1, 92 | 3, 69 | -0, 47 | 0, 9 | |
| 5, 9 | 3, 2 | 10, 24 | 18, 88 | -1, 32 | 1, 74 | -1, 37 | 1, 81 | |
| 7, 6 | 4, 5 | 20, 25 | 34, 2 | -0, 02 | 0, 33 | -0, 01 | ||
| 9, 5 | 5, 1 | 26, 01 | 48, 45 | 0, 58 | 0, 34 | 2, 23 | 1, 29 | |
| 8, 4 | 6, 7 | 44, 89 | 56, 28 | 2, 18 | 4, 75 | 1, 13 | 2, 46 | |
| 10, 1 | 7, 3 | 53, 29 | 73, 73 | 2, 78 | 7, 73 | 2, 83 | 7, 87 | |
| 12, 3 | 8, 9 | 79, 21 | 109, 47 | 4, 38 | 19, 18 | 5, 03 | 22, 03 | |
| Сума | 72, 7 | 45, 2 | 258, 34 | 389, 82 | 54, 04 | 61, 22 |
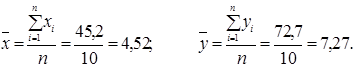
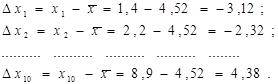
Запишемо систему нормальних рівнянь:
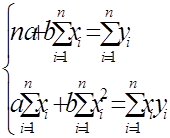
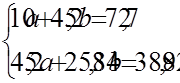
Розв’яжемо її:
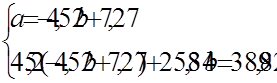
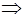
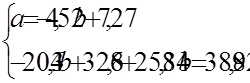
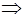
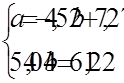
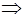
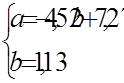
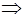
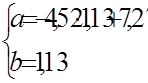
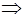
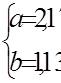
Знайдемо ці ж оцінки за формулами відхилень від середніх (1.9) та (1.10):
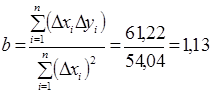 ;
; 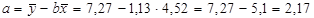 .
.
Отже, нами отримано оціночне рівняння економетричної моделі
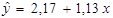 .
.
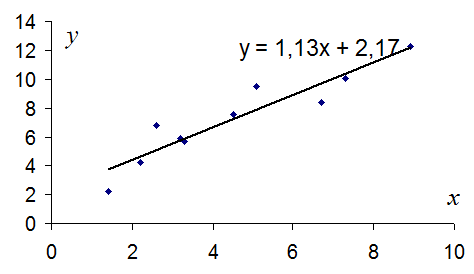 |
3. Побудуємо оціночну пряму
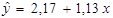 .
.
Рис.1.6. Діаграма розсіювання та оціночна пряма