Властивості оцінок параметрів моделі парної регресії

Розрізняють точкові та інтервальні оцінки параметрів економетричної моделі.

Точковою оцінкою параметра економетричної моделі називають знайдену оцінку цього параметру.

Інтервальною оцінкою параметра економетричної моделі називають інтервал, в межах якого з певною заданою ймовірністю знаходиться істинне значення цього параметру.

Оцінки параметрів економетричної моделі мають такі властивості:

1) Незміщеність.

Вибіркова оцінка b параметра b називається незміщеною, якщо вона задовольняє умову М (b)= b.

2) Обґрунтованість(спроможність).

Вибіркова оцінка b параметра b називається обґрунтованою (спроможною), якщо для як завгодно малого числа e справджується умова

,

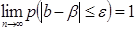тобто при збільшенні об’єму вибірки до безмежності оцінка як завгодно близько наближається до істинного параметру.

Ми бачимо, що оцінка є обґрунтованою, якщо вона задовольняє закон великих чисел. Обґрунтованість помилки означає, що чим більші будуть вибірки, тим більша ймовірність того, що помилка оцінки не перевищує як завгодно малого числа e.

3) Ефективність.

Вибіркова оцінка b параметра b називається ефективною, якщо вона має найменшу дисперсію.

Теорема Гауса-Маркова. Якщо для залишкового члена рівняння (1.1) виконуються умови Гауса-Маркова, то оцінки а і b, розраховані за методом найменших квадратів, мають найменшу дисперсію в класі всіх лінійних незміщених оцінок.

Оцінки а і b, знайдені методом найменших квадратів є незміщеними, ефективними та спроможними.