Способи виявлення мультиколінеарності

Виявити явище мультиколінеарності можна декількома способами:

1) Якщо значення коефіцієнтів парної кореляції між двома незалежними змінними більше 0, 8, то це означає, що між ними існує мультиколінеарність;

2) Якщо значення визначника кореляційної матриці близьке до нуля, то це свідчить про те, що в масиві незалежних змінних існує мультиколінеарність;

3) Якщо невелика зміна (додавання чи відкидання невеликого числа спостережень) приводить до суттєвої зміни значень оцінок параметрів економетричної моделі, чи знаків цих оцінок, то в даному випадку між незалежними змінними може існувати мультиколінеарність;

4) При побудові багатофакторної економетричної моделі ми отримали значення оцінок параметрів, що мають з економічної точки зору невірні знаки або невиправдано великі чи малі значення, то причиною цього може бути явище мультиколінеарності.

На практиці найчастіше для виявлення мультиколінеарності використовують метод Фаррара-Глобера. В основі алгоритму цього методу є три статистичні критерії:

- критерій 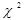, з допомогою якого встановлюємо чи існує мультиколінеарність у всьому масиві незалежних змінних;

- F -критерій Фішера, за яким визначаємо мультиколінеарність кожної незалежної змінної з масивом інших;

- t -критерій Стьюдента, на основі якого перевіряємо наявність мультиколінеарності кожної пари незалежних змінних.

Сам алгоритм методу складається з таких етапів:

1) Обчислюємо емпіричне значення 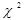за формулою:

,

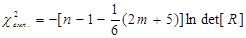де n – об’єм вибірки (кількість спостережень);

m – кількість незалежних змінних;

det[ R ] – визначник кореляційної матриці [ R ];

ln – натуральний логарифм.

2) Для заданої ймовірності p (рівня значимості α =1– p) і числа ступенів вільності 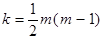знаходимо табличне значення 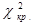Дальше порівнюємо емпіричне і табличне значення. Якщо 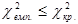, то з заданою ймовірністю p, яку називають довірчою ймовірністю, або надійністю, можна стверджувати, що загальна мультиколінеарність відсутня і дослідження мультиколінеарності на цьому закінчується. Якщо ж 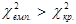, то з заданою надійністю p вважаємо, що в масиві незалежних змінних існує мультиколінеарність.

3) Розраховуємо емпіричне значення параметру F за формулою:

,

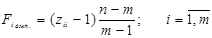де z_ii – елементи головної діагоналі матриці [ Z ], оберненої до кореляційної [ R ].

4) Для заданої ймовірності p (рівня значимості α =1– p) і числа ступенів вільності 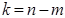знаходимо табличне значення 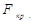Дальше порівнюємо емпіричне і табличне значення. Якщо 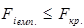, то з заданою ймовірністю p, можна стверджувати, що змінна х_і не мультиколінеарна з масивом інших незалежних змінних. Якщо ж 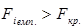, то існує мультиколінеарність змінної х_і з масивом інших незалежних змінних.

5) Знаходимо емпіричне значення параметру:

,

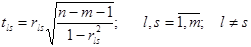де r_ls – коефіцієнти частинної кореляції між незалежними змінними x_l та x_s, значення яких обчислюємо за формулою:

,

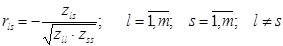а z_ls, z_ll та z_ss – елементи матриці [ Z ].

6) За таблицями Стьюдента для рівня значущості α та числа ступенів вільності 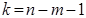знаходимо табличне значення t_кр. і порівнюємо його з емпіричним. Якщо 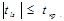, то з заданою ймовірністю p можна стверджувати, що між змінними x_l та x_s немає мультиколінеарності. Якщо ж 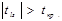, то мультиколінеарність між цими змінними існує.

Таким чином, при побудові багатофакторних економетричних моделей ми можемо встановити, чи існує мультиколінеарність, але перед нами стоїть питання як її позбутися, або зменшити її вплив.