Розв’язування.

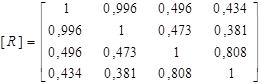
і обчислюємо визначник кореляційної матриці 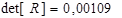. Знаходимо емпіричне значення 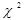за формулою: 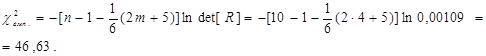За таблицями знаходимо:

.

Оскільки 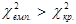, то з ймовірністю p =0, 95 можемо стверджувати, що в масиві незалежних змінних існує мультиколінеарність.

Дальше знаходимо матрицю, обернену до кореляційної

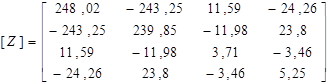
і емпіричні значення параметру F для кожної незалежної змінної:

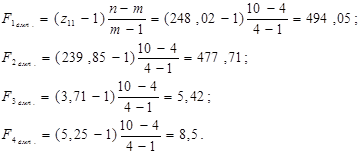
Знаходимо табличне значення 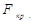=4, 76 (для p =0, 95 і 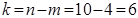) і порівнюємо емпіричне і табличне значення. Оскільки 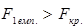та 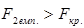, то робимо висновок, що змінні х₁ та х₂ мультиколінеарні з масивом інших незалежних змінних.

Перевіримо між якими саме парами незалежних змінних існує мультиколінеарність з допомогою критерію Стьюдента. Знайдемо коефіцієнти частинної кореляції:

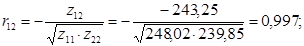
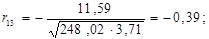
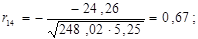
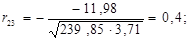
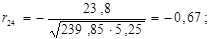
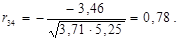
Дальше розраховуємо емпіричні значення параметру t для кожної пари незалежних змінних:

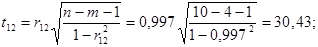
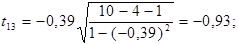
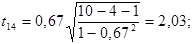
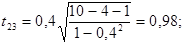
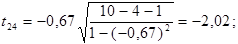
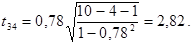
За таблицями Стьюдента для рівня значущості α =0, 05 та числа ступенів вільності 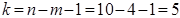знаходимо табличне значення t_кр =2, 447 _. і порівнюємо його з емпіричним. Оскільки 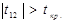, то існує мультиколінеарність між змінними х₁ та х₂, 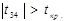, значить змінні х₃ та х₄ теж мультиколінеарні. Виключимо з масиву незалежних змінних х₂ і перевіримо, чи існує ще мультиколінеарність в масиві змінних, що залишилися.

Знаходимо елементи нової кореляційної матриці

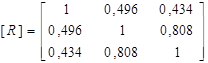
визначник якої 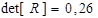. Емпіричне значення :

.

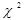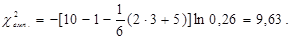
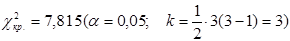Оскільки 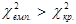, то в масиві незалежних змінних ще існує мультиколінеарність.

Матриця, обернена до кореляційної

.

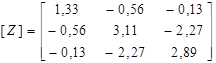Тоді

,

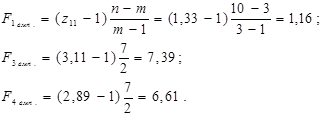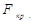=4, 74 (для p =0, 95 і 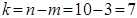). Оскільки 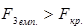та 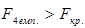, то змінні х₃ та х₄ мультиколінеарні з масивом інших незалежних змінних.

Знаходимо коефіцієнти частинної кореляції:

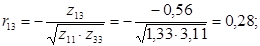
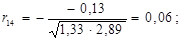
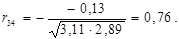
Дальше розраховуємо емпіричні значення параметру t для кожної пари незалежних змінних:

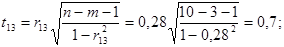
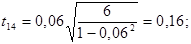
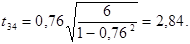
t_кр =2, 365 _. (для α =0, 05 і 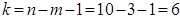). 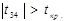, значить існує мультиколінеарність між змінними х₃ та х₄. Виключимо з масиву незалежних змінних х₄ і перевіримо, чи існує ще мультиколінеарність між змінними х₁ та х₃.

.

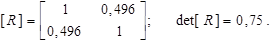
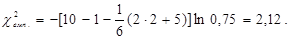
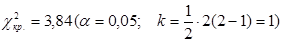Оскільки 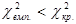, то в масиві незалежних змінних немає мультиколінеарністі.

Слід зазначити, що при дослідженні мультиколінеарності використання критерію Фішера не обов’язкове, оскільки інколи з його допомогою не можна визначити, яку із незалежних змінних потрібно виключати з розгляду. Точну відповідь на це питання ми отримуємо за критерієм Стьюдента.

Тепер залишається побудувати економетричну модель (оціночне рівняння) залежності прибутку від вартості основних виробничих фондів та ціни одиниці продукції. Алгоритм побудови оціночного рівняння багатофакторної економетричної моделі подано в п.2.2. (приклад 2.1). Зауважимо, що оцінки параметрів економетричної моделі можна знайти також, використавши стандартну офісну програму EXCEL (Сервис – Анализ данных – Регрессия).