Умови Гаусса-Маркова для випадкової змінної

При використанні МНК для знаходження оцінок параметрів моделі випадкова змінна (збурення, випадковий член) повинна задовольняти чотири умови, що мають назву умови Гаусса-Маркова.

1. Математичне сподівання випадкової змінної для всіх спостережень рівне нулю:

M (u_i)=0,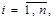

де n – кількість спостережень.

Інколи випадковий член моделі може бути додатнім, а інколи – від’ємним. Однак він не має мати систематичного зміщення в жодному можливому напрямку.

2. Дисперсія випадкової змінної повинна бути постійною для всіх спостережень (властивість гомоскедастичності):

.

3. Відсутність систематичного зв’язку між значеннями випадкової змінної в будь-яких спостереженнях:

.

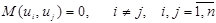Це означає, що випадкові величини незалежні між собою, тобто значення випадкової змінної u в і -му спостереженні не залежить від того, яке значення вона прийме в j –му спостереженні.

4. Випадкова змінна повинна бути розподіленою незалежно від пояснюючих змінних:

Значення будь-якої незалежної змінної в кожному спостереженні вважається екзогенним, повністю визначеним зовнішніми причинами, які не враховані в рівнянні регресії.

Крім приведених вище умов припускається дотримання нормального закону розподілу випадкового члена з нульовим математичним сподіванням і постійною дисперсією. Припущення про нормально розподілені величини ґрунтується на центральній граничній теоремі, яка стверджує, що, якщо випадкова величина є загальним результатом взаємодії значного числа інших випадкових величин, то вона буде мати приблизно нормальний розподіл, навіть якщо окремі складові не матимуть його.