Додатна регресія

Від’ємна регресія

Рис. 1.3. Основні форми регресій

Отже, розрізняють додатну лінійну (а) та нелінійну (б, в) і від’ємну лінійну (г) та нелінійну (д, е) регресії.

За виглядом скупчення точок можна висунути гіпотезу про лінійність чи нелінійність взаємозв’язку між змінними. Так, на діаграмі 1.3 (а, г) маємо явно виражені лінійні тенденції скупчення точок. Спробуємо апроксимувати залежності, зображені на цих діаграмах, лінійною функцією регресії. Звичайно, ці тенденції існують лише в середньому. Вони порушені відхиленням окремих точок. Відхилення від прямої пояснюється впливом інших неврахованих факторів.

3. Модель парної лінійної регресії

Припустимо, що за виглядом діаграми розсіювання ми встановили, що між двома змінними існує лінійний зв’язок. Проста (парна) лінійна регресія встановлює лінійну залежність між двома змінними. При цьому одна із змінних (у) вважається залежною змінною (екзогенна, пояснювана, результативна змінна, регресант, відгук) і розглядається як функція від другої (х) незалежної змінної (ендогенна, пояснююча, регресор).

В загального випадку проста лінійна модель запишеться так:

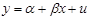(1.1)

Величина у= { у₁, у₂ ,.., у_n } (n – число спостережень) складається з двох складових:

1) невипадкової складової a+bх, де х={х₁, х₂,.., х_n}, a і b – параметри рівняння;

2) випадкової складової u (збурення, помилки) u={u₁, u₂,.., u_n}.

Якщо у та х – це кількісні показники деяких економічних явищ чи процесів, то рівняння (1.1) називають економетричною моделлю.

Розглянемо основні причини існування збурення:

1. Невключення в модель інших пояснюючих змінних. Встановлення зв’язку тільки між двома факторами у та х є дуже великим спрощенням. Наспрaвді існують інші фактори, що суттєво впливають на результативний показник, які не враховані чи не можуть бути врахованими у формулі (1.1). Вплив цих факторів приводить до того, що істинні точки лежать поза прямою. Об’єднавши всі такі можливі складові впливу на результативний показник, ми якраз отримаємо величину u. Наприклад, при вивченні залежності попиту на товар (у) від ціни на товар (х), збурена змінна u включала би в себе вплив на попит таких чинників: величина сімейного бюджету, якість товару та інші випадкові фактори. Якби ми точно знали, які змінні необхідно включати в модель, і мали можливість точно їх виміряти, то можна на їх основі будувати рівняння і тим самим виключати відповідний елемент збурення.

2. Неправильна функціональна специфікація. Функціональне співвідношення між у та х математично може бути визначене неправильно. Наприклад, фактична залежність не є лінійною, а може бути більш складною. Проте, використання рівняння регресії, яке найкраще описує залежність між змінними є деяким наближенням.

3. Помилки вимірювання. Якщо у вимірюваннях однієї чи більше взаємозв’язаних змінних є помилки, то знайдені значення не будуть відповідати точному співвідношенню, а існуюча розбіжність буде вносити свій вклад у структуру збуреної змінної.

4. Людський фактор, який неможливо математично описати і нічим, крім випадкової складової відобразити не можна. Наприклад, при встановленні залежності попиту на товар від ціни на нього це можуть бути вподобання покупця.

Отже, збурення є сумарним проявом перелічених вище факторів.

Практично побудувати економетричну модель у вигляді рівняння (1.1) неможливо через випадкову складову, тому лінійну залежність між двома змінними будують у вигляді оціночного рівняння економетричної моделі, відкинувши випадкову складову:

, (1.2)

де a та b відповідно, представляють собою оцінки параметрів a та b рівняння (1.1). Знак “^” над у означає оцінку залежної змінної, отриману з рівняння (1.2) при деяких усереднених умовах.

Розглянемо геометричну інтерпретацію оцінок параметрів економетричної моделі.

Рис. 1.4. Регресійна пряма та її параметри

Постійна величина а визначає точку перетину прямої регресії з віссю ординат (рис. 1.4) і є значенням у в точці х₀ =0.

Коефіцієнт b характеризує нахил прямої до осі абсцис. Позначимо через a кут, який пряма утворює з віссю абсцис. Тоді b =tg a. Він є мірою залежності змінної у від х або мірою впливу, виявленою зміною х на у. Відповідно до рівняння (1.2) b визначає середню величину зміни результативного показника при зміні пояснювальної змінної х на одиницю. Знак b визначає напрямок цієї зміни.

Після визначення числових оцінок параметрів можна за рівнянням (1.2) обрахувати значення 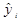для кожного значення пояснюючої змінної х_і. Це значення називають розрахунковим.

При лінійній функції сукупність розрахункових значень утворює пряму регресії. Як відзначалося раніше, через випадковий вплив сторонніх факторів для кожного значення х_і може спостерігатися декілька емпіричних значень у_і, тобто кожному значенню х відповідає розподіл значень змінної у. Значення функції регресії таким чином є оцінками середніх значень змінної у для кожного фіксованого значення змінної х.

Звідси випливає економічна інтерпретація . Значення показують середнє значення залежної змінної у при заданому х_і пояснюючої змінної у припущенні, що єдиною причиною зміни у є змінна х, а випадкова збурена змінна u прийняла значення, рівне нулеві. Розкид фактичних значень змінної у довкола зумовлений впливом множини неврахованих факторів. Різницею між емпіричним значенням у_і і розрахунковим 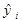назвемо залишком, який дає числову оцінку значенням збуреної змінної u (рис. 1.4). Отже, числове значення е визначається як 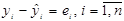. Зрозуміло, що, чим менше значення е_і, тим вдаліше вибрана пряма.

Таким чином, ми підійшли до проблеми оцінювання невідомих параметрів a та b.