
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическая модель оптимизации прибыли с учетом штрафа
|
|
Обратимся к третьему критерию оптимальности, равному разности общей прибыли предприятия от реализации готовой продукции и штрафа за простой оборудования. Математически задача состоит в максимизации функции
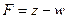 (1.8)
(1.8)
при ограничениях (1.3)-(1.4).
Используя соотношения (1.5) и (1.7), получим
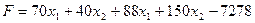 .
.
Тогда модель задачи состоит в определении чисел 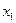 и
и 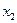 , удовлетворяющих системе ограничений (1.3)-(1.4), для которых целевая функция
, удовлетворяющих системе ограничений (1.3)-(1.4), для которых целевая функция
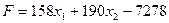 (1.9)
(1.9)
достигает максимума. Решение этой задачи выполним в Excel на третьем листе, как показано в табл. 1.8. Целевой ячейкой является G11, содержимое которой определяется формулой
= D11 – G10,
вытекающей из (1.8).
Т а б л и ц а 1.8
| A | B | C | D | E | F | G | |
| Целевая функция 3 – прибыль - штраф | |||||||
| Продукция | Шкаф | Стол | |||||
| Значение | |||||||
| Ограничения | |||||||
| Станки | Левая часть | Знак | Правая часть | Штраф | |||
| Строгальные | < = | ||||||
| Фрезерные | < = | ||||||
| Шлифовальные | < = | ||||||
| ЦФ1 | ЦФ2 | ||||||
| Прибыль | ЦФ3-> max |
Поиск решения дает оптимальное решение по третьему критерию (ячейки B4: C4), которое состоит в выпуске шкафов и столов в количествах 22 и 34 ед. Максимальная прибыль с учетом штрафа за простой оборудования (ячейка G11) равна 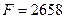 ден.ед.
ден.ед.
Аналогично можно определить оптимальный план выпуска продукции с учетом штрафа, используя выражение (1.9).
Содержание отчета по работе
Отчет должен содержать следующие пункты:
· задание на работу с конкретными исходными данными студента,
· математическую модель максимизации прибыли,
· математическую модель минимизации штрафа,
· графическое решение задачи максимизации прибыли,
· оптимизацию общей прибыли в Excel в табличном виде,
· оптимизацию штрафа в Excel в табличном виде,
· математическую модель и оптимизацию прибыли с учетом штрафа,
· выводы по работе.