
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графическое решение задачи максимизации приыли
|
|
На рис. 1.1 приведено графическое решение задачи по критерию (1.5). На основе системы ограничений (1.3)–(1.4) строится допустимая область в виде многоугольника OABCD. Покажем, например, как построена прямая I. В уравнении 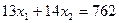 положим
положим 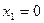 , тогда получим
, тогда получим 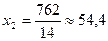 . Затем положим
. Затем положим 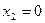 , тогда
, тогда 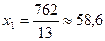 . Через две точки проведем прямую I. Неравенство
. Через две точки проведем прямую I. Неравенство 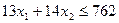 определяет полуплоскость, расположенную ниже этой прямой. Аналогично неравенство
определяет полуплоскость, расположенную ниже этой прямой. Аналогично неравенство 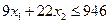 задает полуплоскость, расположенную под прямой II, а неравенство
задает полуплоскость, расположенную под прямой II, а неравенство 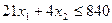 – полуплоскость, расположенную левее прямой III. Условия неотрицательности (1.4) в совокупности определяют первый квадрант координатной плоскости.
– полуплоскость, расположенную левее прямой III. Условия неотрицательности (1.4) в совокупности определяют первый квадрант координатной плоскости.
Оптимальное решение задачи по первому критерию определяется следующим образом. Строится вектор 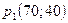 , координаты которого равны (или пропорциональны) коэффициентам целевой функции (1.5). Перпендикулярно этому вектору изображается прямая (линия уровня целевой функции), которая перемещается в направлении вектора, пока прямая имеет общие точки с допустимой областью. Оптимальное решение по первому критерию есть точка пересечения допустимой области с линией уровня, отвечающей максимальному значению
, координаты которого равны (или пропорциональны) коэффициентам целевой функции (1.5). Перпендикулярно этому вектору изображается прямая (линия уровня целевой функции), которая перемещается в направлении вектора, пока прямая имеет общие точки с допустимой областью. Оптимальное решение по первому критерию есть точка пересечения допустимой области с линией уровня, отвечающей максимальному значению 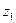 . Это есть вершина
. Это есть вершина 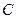 . Координаты точки
. Координаты точки 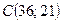 определяются по графику приближенно. Они дают оптимальное решение задачи по первому критерию.
определяются по графику приближенно. Они дают оптимальное решение задачи по первому критерию.
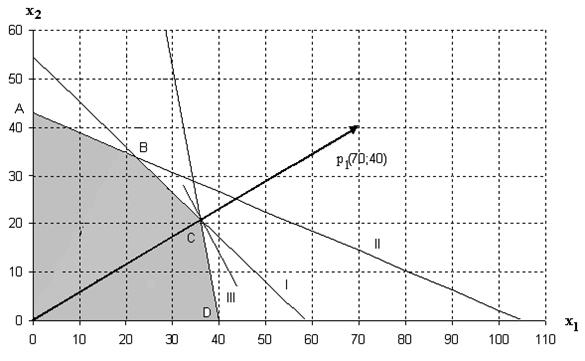
Рис. 1.1. Графическое решение задачи по первому критерию
Таким образом, выпуск продукции в количествах 36 и 21 ед. соответственно обеспечивает предприятию максимальную общую прибыль. Построение допустимой области можно выполнить в Excel. Для этого в соответствии с уравнениями системы (1.3) образуем табл. 1.3. В блок ячеек A3: A14 введем значения аргумента 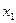 , изменяющегося от нуля до
, изменяющегося от нуля до 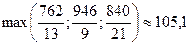 .
.
Т а б л и ц а 1.3
| A | B | C | D | ||
| 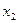
| ||||
| Прямая I | Прямая II | Прямая III | |||
| 54, 43 | |||||
| 45, 14 | 38, 9 | ||||
| 35, 86 | 34, 8 | ||||
| 26, 57 | 30, 7 | 52, 5 | |||
| 17, 29 | 26, 6 | ||||
| 22, 5 | –53 | ||||
| –1, 29 | 18, 5 | –105 | |||
| –10, 6 | 14, 4 | –158 | |||
| –19, 9 | 10, 3 | –210 | |||
| –29, 1 | 6, 18 | –263 | |||
| –38, 4 | 2, 09 | –315 | |||
| –47, 7 | –2 | –368 |
В ячейки B3, C3 и D3 введем формулы из табл. 1.4, которые копируются на блок ячеек B4: D14.
Т а б л и ц а 1.4
| B3 | = (762 – 13 * A3) / 14 |
| C3 | = (946 – 9 * A3) / 22 |
| D3 | = (840 – 21 * A3) / 4 |
С помощью мастера диаграмм и блока ячеек B3: D14 из табл. 1.3 строятся графики прямых линий I, II и III. Используя пункт меню «Ряд» и «Подписи оси x», указывают значения аргумента 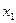 , содержащиеся в блоке ячеек A3: A14. После построения прямых следует выделить допустимую область, ограничив диаграмму снизу и сверху по вертикальной оси. Путем изменения размеров графика необходимо добиться, чтобы масштаб по осям координат был одинаковым. Подписи данных удобно сделать, используя пункт меню «Вид / Панели инструментов / Рисование».
, содержащиеся в блоке ячеек A3: A14. После построения прямых следует выделить допустимую область, ограничив диаграмму снизу и сверху по вертикальной оси. Путем изменения размеров графика необходимо добиться, чтобы масштаб по осям координат был одинаковым. Подписи данных удобно сделать, используя пункт меню «Вид / Панели инструментов / Рисование».