
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сведения из теории. Область математики, занимающаяся исследованием и решением задач нахождения наибольших или наименьших значений функций на конечных (или счетных) множествах
|
|
Область математики, занимающаяся исследованием и решением задач нахождения наибольших или наименьших значений функций на конечных (или счетных) множествах, называется дискретным программированием. Наиболее изученными задачами этого раздела являются целочисленные задачи линейного программирования, т.е. задачи линейного программирования, в которых на все переменные или на их часть наложено дополнительное требование целочисленности. Аналогичным образом определяются целочисленные задачи и для более общих задач оптимального программирования – можно говорить, например, о задачах выпуклого целочисленного программирования и т.д. От целочисленных задач принято отличать так называемые дискретные задачи математического программирования, в которых областью допустимого изменения переменных является не множество целых неотрицательных чисел, а некоторое произвольное конечное множество. Однако формально такие задачи могут быть сведены к целочисленным. Здесь будут рассматриваться лишь модели линейного целочисленного программирования.
В моделях линейного целочисленного программирования по сравнению с обычными моделями линейного программирования на все переменные величины 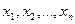 или на некоторые из них налагается требование целочисленности. В первом случае обычно говорят о полностью целочисленных, а во втором - о частично целочисленных задачах.
или на некоторые из них налагается требование целочисленности. В первом случае обычно говорят о полностью целочисленных, а во втором - о частично целочисленных задачах.
Значительная часть задач экономического характера требует целочисленности решений. Различают две разновидности моделей задач линейного целочисленного программирования: задачи с неделимостью и задачи с булевыми переменными. К первым относятся модели задач, в которых искомые величины являются физически неделимыми объектами, как, например, число предприятий, число распределяемых машин, количество единиц неделимой информации и т.п. Модели с булевыми переменными (т.е. переменными, принимающими два значения " 0" или " 1") охватывают разнообразные оптимальные задачи комбинаторного характера, задачи с дополнительными логическими условиями, которые с помощью искусственно вводимых булевых переменных приводятся к линейным моделям задач целочисленного программирования.
Оптимальное решение, найденное симплексным методом, как правило, не является целочисленным. Округление полученных результатов до ближайших целых чисел допустимо в тех случаях, когда значения переменных, образующих оптимальный план исходной задачи, достаточно велики, и погрешностями округления с практической точки зрения можно пренебречь. Однако, во многих случаях такое округление дает вообще недопустимое решение, а если решение оказывается допустимым, то далеко не лучшим среди целочисленных решений, т.е. не оптимальным. Поэтому для нахождения оптимального целочисленного решения нужны особые методы и алгоритмы.
Методы целочисленной оптимизации можно разделить на три основные группы: методы отсечений, комбинаторные методы и приближенные методы. Название " методы отсечений" связано с тем обстоятельством, что в систему ограничений вводятся дополнительные неравенства, отсекающие некоторые части множества допустимых решений, в которых отсутствуют точки с целочисленными координатами. Комбинаторные методы занимают доминирующее положение в целочисленном программировании. Это методы направленного частичного перебора допустимых решений. Наиболее известным комбинаторным методом является метод ветвей и границ, в котором из рассматриваемой задачи получается две подзадачи путем специального разбиения множества допустимых решений и отбрасывания областей, не содержащих целочисленных решений. Трудности машинной реализации точных методов решения задач целочисленного программирования привели к появлению приближенных методов случайного поиска в сочетании с локальной оптимизацией, а также методов, построенных на использовании особенностей конкретной задачи.
Среди задач целочисленной оптимизации исключительно важными для практики являются, так называемые, раскройные задачи. В этих задачах требуется наилучшим образом произвести раскрой каких-либо материалов. Это могут быть бревна, брус, прутья, арматура и другие одномерные материалы. Раскрой может быть двумерный или плоский, если требуется раскроить плиты (древесно-стружечные, древесно-волокнистые и пр.), фанеру, стекло, линолеум и другие материалы. Моделирование оптимального раскроя материалов является одним из способов эффективного использования производственных ресурсов предприятия.