
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сведения из теории. Планирование перевозок грузов является важной экономической задачей, занимающей ключевое место среди других проблем планирования
|
|
Планирование перевозок грузов является важной экономической задачей, занимающей ключевое место среди других проблем планирования. Большое значение имеет задача о минимизации транспортных издержек при перевозках однородных грузов из пунктов производства в пункты потребления, например, древесины с нижних складов к деревообрабатывающим предприятиям, строительных материалов с баз на стройплощадки и т.п.
Пусть 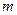 поставщиков
поставщиков 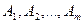 располагают
располагают 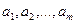 единицами некоторого однородного продукта (груза), и этот продукт должен быть доставлен
единицами некоторого однородного продукта (груза), и этот продукт должен быть доставлен 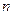 потребителям
потребителям 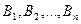 в количествах
в количествах 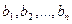 соответственно. Известны стоимости
соответственно. Известны стоимости 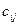 ,
,  ,
, 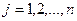 перевозки единицы груза от поставщика
перевозки единицы груза от поставщика 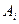 потребителю
потребителю 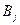 . Следует определить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности и имеющий наименьшие суммарные транспортные затраты.
. Следует определить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности и имеющий наименьшие суммарные транспортные затраты.
Модель транспортной задачи называется закрытой (или сбалансированной), если суммарные запасы груза равны суммарным потребностям, т.е.
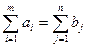 . Если это условие не выполняется, то модель называется открытой (или несбалансированной). Открытая модель легко сводится к закрытой путем введения фиктивного поставщика (если потребности превышают запасы) или фиктивного потребителя (если запасы превышают потребности). Поэтому мы ограничимся рассмотрением только закрытой модели.
. Если это условие не выполняется, то модель называется открытой (или несбалансированной). Открытая модель легко сводится к закрытой путем введения фиктивного поставщика (если потребности превышают запасы) или фиктивного потребителя (если запасы превышают потребности). Поэтому мы ограничимся рассмотрением только закрытой модели.
План перевозок транспортной задачи можно представить в виде матрицы 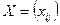 , где
, где 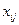 – количество единиц груза, перевозимого от поставщика
– количество единиц груза, перевозимого от поставщика 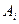 потребителю
потребителю 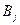 ,
,  ,
, 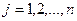 . Естественно предполагать, что
. Естественно предполагать, что 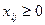 .
.
Стоимость перевозки груза от 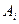 к
к 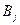 составит
составит 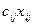 . Следовательно, суммарные транспортные расходы по плану
. Следовательно, суммарные транспортные расходы по плану 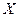 составят
составят
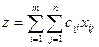 . (3.1)
. (3.1)
Система ограничений получается из следующих соображений. Все запасы из пункта 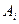 должны быть вывезены, т.е.
должны быть вывезены, т.е.
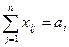 ,
,  . (3.2)
. (3.2)
Все потребности пункта 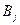 должны быть удовлетворены, т.е.
должны быть удовлетворены, т.е.
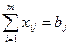 ,
, 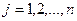 . (3.3)
. (3.3)
Таким образом, математическая модель транспортной задачи состоит в определении неотрицательного плана перевозок 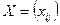 , для которого выполняются условия (3.2) и (3.3), а целевая функция (3.1) принимает наименьшее значение. Доказано, что транспортная задача с закрытой моделью всегда разрешима, т.е. она имеет оптимальное решение.
, для которого выполняются условия (3.2) и (3.3), а целевая функция (3.1) принимает наименьшее значение. Доказано, что транспортная задача с закрытой моделью всегда разрешима, т.е. она имеет оптимальное решение.
Специфика ограничений транспортной задачи значительно облегчает применение симплексного метода для ее решения. Симплексный метод сводится к методу потенциалов, при использовании которого можно обойтись без составления симплексных таблиц, заменив их таблицами перевозок вида табл. 3.1.
Т а б л и ц а 3.1
| Пункты отправления и запасы груза | Пункты назначения и потребности | |||||||
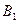
| 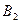
| … | 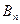
| |||||
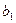
| 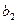
| … | 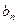
| |||||
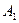
| 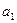
| 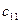
| 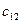
| … | 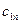
| |||
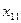
| 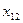
| 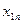
| ||||||
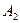
| 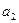
| 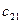
| 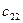
| … | 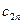
| |||
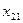
| 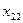
| 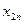
| ||||||
| … | … | … | … | … | … | |||
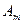
| 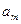
| 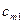
| 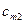
| … | 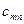
| |||
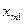
| 
| 
|