
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сведения из теории. Важный раздел целочисленной оптимизации составляют математические модели задач с булевыми переменными
|
|
Важный раздел целочисленной оптимизации составляют математические модели задач с булевыми переменными, т.е. переменными, принимающими только два значения " 1", или " 0". С помощью булевых переменных можно решать самые различные по содержанию задачи, в которых надо что-то выбирать из имеющихся различных вариантов. Примерами задач данного класса в процессе управления производством служат задачи
· оптимального назначения исполнителей на работы,
· при выборе вариантов комплектующих изделий,
· при выборе типа станка для обработки деталей,
· в задаче закрепления продавцов за товарами различных видов, и т.д.
Для того, чтобы составить матрицу условий задачи необходимо иметь исходные данные: характеристики деятельности любого исполнителя на каждой работе, определяющие значение принятого критерия оптимальности. Так, в задаче закрепления продавцов за товарами должны быть известны доходы каждого продавца от продажи товара любого вида, т.е. должна быть известна матрица
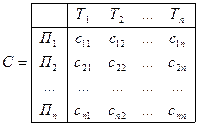 .
.
Продавцам 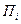 соответствуют строки, а видам товаров
соответствуют строки, а видам товаров 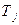 – столбцы этой матрицы. В задаче требуется определить, за каким продавцом должен быть закреплен тот или иной товар, т.е. ответить на вопрос «будет ли
– столбцы этой матрицы. В задаче требуется определить, за каким продавцом должен быть закреплен тот или иной товар, т.е. ответить на вопрос «будет ли 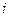 -ый продавец продавать
-ый продавец продавать 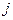 -ый товар или не будет». Таким образом, искомые неизвестные должны принимать только два значения «да», или «нет». В числовом выражении «1», или «0».
-ый товар или не будет». Таким образом, искомые неизвестные должны принимать только два значения «да», или «нет». В числовом выражении «1», или «0».
Для составления математической модели введем булевы переменные 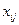 следующим образом:
следующим образом: 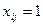 , если
, если 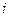 -ый продавец осуществляет продажу
-ый продавец осуществляет продажу 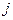 -го товара, и
-го товара, и 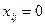 , если
, если 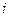 -ый продавец не занят продажей
-ый продавец не занят продажей 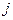 -го товара. В сокращенном виде
-го товара. В сокращенном виде
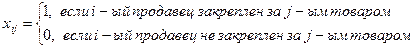 ,
, 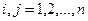 .
.
Запишем булевы неизвестные в виде следующей матрицы
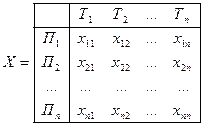 .
.
Через 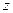 обозначим суммарный доход от продажи всего товара. Тогда
обозначим суммарный доход от продажи всего товара. Тогда
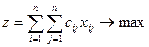 . (4.1)
. (4.1)
Так как по условию каждый продавец продает только один вид товара, то
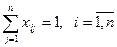 . (4.2)
. (4.2)
Так как каждый вид товара реализуется одним продавцом, то
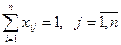 . (4.3)
. (4.3)
Таким образом, математическая модель задачи о назначениях состоит в определении неотрицательных целых чисел 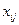 , удовлетворяющих ограничениям (4.2)-(4.3), для которых целевая функция (4.1) максимальна. Система ограничений задачи показывает, что каждое допустимое решение можно представить матрицей, содержащей по одной единице в каждой строке и каждом столбце, а остальные элементы матрицы равны нулям. Ясно также, что число допустимых решений в задаче равно
, удовлетворяющих ограничениям (4.2)-(4.3), для которых целевая функция (4.1) максимальна. Система ограничений задачи показывает, что каждое допустимое решение можно представить матрицей, содержащей по одной единице в каждой строке и каждом столбце, а остальные элементы матрицы равны нулям. Ясно также, что число допустимых решений в задаче равно 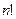 , и поэтому допустимое множество дискретно.
, и поэтому допустимое множество дискретно.
Математическая модель в виде (4.1)-(4.3) представляет собой классический вариант задачи о назначениях. Она относится к линейному целочисленному программированию с булевыми переменными. В принципе комбинаторные задачи приведенного вида могут быть решены полным перебором всехвозможных вариантов допустимых решений. Однако, количество этих вариантов может быть столь большим, что полный перебор невозможно осуществить в реальноне время даже с помощью современных ЭВМ. Так, при 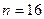 получим число допустимых решений
получим число допустимых решений 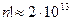 . Если предположить, что компьютер в течение 1с находит
. Если предположить, что компьютер в течение 1с находит 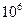 допустимых решений и для каждого из них вычисляет значение целевой функции, то для решения задачи потребуется
допустимых решений и для каждого из них вычисляет значение целевой функции, то для решения задачи потребуется 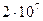 с, или
с, или 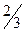 года (
года (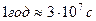 ). Таким образом, для решения данной задачи при больших значениях
). Таким образом, для решения данной задачи при больших значениях 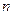 перебор допустимых решений неприменим.
перебор допустимых решений неприменим.
Заметим, что математическая модель задачи о назначениях представляет собой частный случай сбалансированной транспортной модели при дополнительном условии целочисленности неизвестных. Поэтому для ее решения может быть применен классический метод решения – метод потенциалов. Для решения задачи можно использовать также венгерский метод и метод ветвей и границ. Однако, при наличии программного обеспечения быстрее и проще использовать информационные технологии.