
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения работы. На двух станках могут обрабатываться детали трех видов
|
|
На двух станках могут обрабатываться детали трех видов. В течение рабочего дня на первом станке может быть обработано 30 деталей первого вида, или 30 деталей второго вида, или 42 детали третьего вида. На втором станке в течение рабочего дня может быть обработано 18 деталей первого вида, или 50 деталей второго вида, или 150 деталей третьего вида.
Пусть 2 детали первого вида, 5 деталей второго вида и 3 детали третьего вида составляют один полный комплект. Определить оптимальный план работы станков, то есть указать, какую часть рабочего дня каждый станок должен обрабатывать детали каждого вида с тем, чтобы число комплектов деталей было наибольшим.
Перечисленные данные запишем в табл. 5.2.
Т а б л и ц а 5.2
| Станки | Детали | ||
| I | |||
| II | |||
| Комплектность | 2: 5: 3 |
Составим математическую модель станковой задачи. Пусть 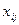 – часть рабочего дня, в течение которой на
– часть рабочего дня, в течение которой на 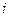 -м станке обрабатываются детали
-м станке обрабатываются детали 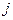 -го вида,
-го вида, 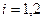 ,
, 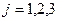 . Тогда план работы станков можно представить таблицей
. Тогда план работы станков можно представить таблицей
| X = | Станки | Детали | |
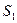
| 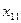
| 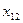
| 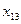
|
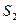
| 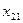
| 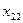
| 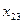
|
Обозначим через 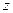 число комплектов деталей, которое будет получено в соответствии с этим планом.
число комплектов деталей, которое будет получено в соответствии с этим планом.
Поскольку рабочий день принят за единицу, то имеем систему ограничений на время работы каждого станка
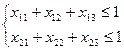 . (5.4)
. (5.4)
Условия неотрицательности неизвестных:
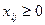 ,
, 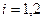 ,
, 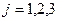 . (5.5)
. (5.5)
Чтобы составить целевую функцию, найдем количество деталей каждого вида, обработанных двумя станками по плану 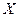 :
:
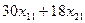 – количество деталей первого вида,
– количество деталей первого вида,
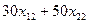 – количество деталей второго вида,
– количество деталей второго вида,
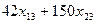 – количество деталей третьего вида.
– количество деталей третьего вида.
Так как один комплект состоит из 2 деталей первого вида, 5 деталей второго вида и 3 деталей третьего вида, то общее число комплектов деталей выражается функцией
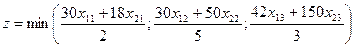 . (5.6)
. (5.6)
Таким образом, математической моделью станковой задачи является задача максимизации целевой функции (5.6) при условиях (5.4)-(5.5).
Рассмотрим два плана обработки деталей. По плану
| X1 = | Станки | Детали | |
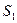
| 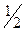
| 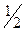
| 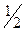
|
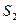
| 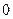
| 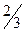
| 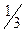
|
число комплектов деталей составляет
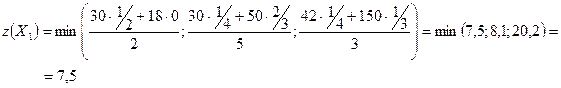 .
.
Так как число комплектов должно быть целым, то считаем, что 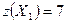 .
.
Второй (оптимальный) план получим с помощью процедуры «Поиск решения» табличного процессора Excel. Математическая модель станковой задачи может быть сведена к задаче линейного программирования. Действительно, из определения целевой функции (4.12) следует, что
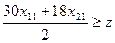 ,
, 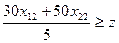 ,
, 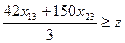 . (5.7)
. (5.7)
При этом число
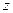 – целое. (5.8)
– целое. (5.8)
Поэтому, если включить 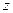 в число неизвестных, то получим математическую модель в виде задачи максимизации функции
в число неизвестных, то получим математическую модель в виде задачи максимизации функции 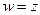 при ограничениях (5.4), (5.5), (5.7), (5.8). Эта модель относится к линейному частично целочисленному программированию. Решение задачи выполним в Excel. В ячейки серого цвета, как показано в табл. 5.3, поместим неизменяемую информацию. В блок ячеек B3: D5 поместим исходные данные задачи, а именно, число обработанных деталей каждым станком в течение рабочего дня и комплектность деталей. Блок ячеек B8: D9 и ячейку F12 предусмотрим для значений оптимального плана работы станков
при ограничениях (5.4), (5.5), (5.7), (5.8). Эта модель относится к линейному частично целочисленному программированию. Решение задачи выполним в Excel. В ячейки серого цвета, как показано в табл. 5.3, поместим неизменяемую информацию. В блок ячеек B3: D5 поместим исходные данные задачи, а именно, число обработанных деталей каждым станком в течение рабочего дня и комплектность деталей. Блок ячеек B8: D9 и ячейку F12 предусмотрим для значений оптимального плана работы станков 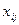 и значения
и значения 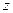 . Эти ячейки оставляем пустыми. В ячейки E8: E9 поместим формулы для записи левых частей системы (5.4), а именно,
. Эти ячейки оставляем пустыми. В ячейки E8: E9 поместим формулы для записи левых частей системы (5.4), а именно,
= СУММ(B8: D8)
и
= СУММ(B9: D9).
В ячейки G8: G9 поместим 1 – правые части системы (5.4). В блок ячеек B12: D12 поместим выражения для левых частей неравенств (5.7). Для этого в ячейку B12 запишем формулу
= СУММПРОИЗВ(B3: B4; B8: B9) / B5
и протянем ее на ячейки C12, D12. Наконец, в ячейку G12 поместим «короткую» формулу для целевой функции
= F12.
Т а б л и ц а 5.3
| A | B | C | D | E | F | G | |||
| Количество обработанных деталей вида | |||||||||
| Станки | |||||||||
| Комплект-ность | |||||||||
| Время обработки деталей | Левая часть | Знак | Правая часть | ||||||
| 0, 666667 | 0, 333333 | < = | |||||||
| 0, 8 | 0, 2 | < = | |||||||
| Число комплектов | Знак | z | ЦФ max | ||||||
| > = | |||||||||
После заполнения табл. 5.3 следует обратиться к процедуре «Поиск решения» и заполнить появившееся окно информацией, указанной на рис. 5.2.
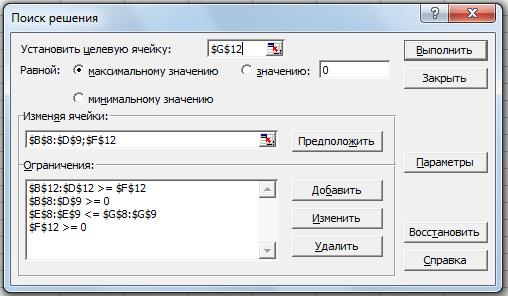
Рис. 5.2. Обращение к процедуре «Поиск решения»
в задаче о комплектном выпуске продукции
Результатом решения задачи в Excel служит оптимальный план обработки деталей, полученный в табл. 5.3.
| Xmax = | Станки | Детали | |
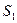
| 0, 67 | 0, 33 | 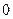
|
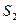
| 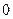
| 0, 8 | 0, 2 |
Для этого плана число полных комплектов деталей равно 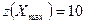 . На рис. 5.3 помещена диаграмма, которая для каждого станка показывает часть рабочего дня, в течение которой согласно оптимальному плану он должен быть занят обработкой деталей.
. На рис. 5.3 помещена диаграмма, которая для каждого станка показывает часть рабочего дня, в течение которой согласно оптимальному плану он должен быть занят обработкой деталей.
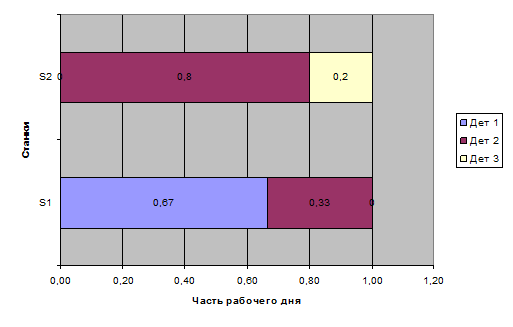 Рис. 5.3. Линейчатая диаграмма с накоплением На диаграмме каждому станку соответствует прямоугольник длины 1 (рабочий день) с разбивкой на доли времени, отведенного на обработку деталей трех видов.
Рис. 5.3. Линейчатая диаграмма с накоплением На диаграмме каждому станку соответствует прямоугольник длины 1 (рабочий день) с разбивкой на доли времени, отведенного на обработку деталей трех видов.
Содержание отчета по работе
Отчет должен содержать следующие пункты:
· задание на работу с конкретными исходными данными студента,
· математическую модель задачи в виде максиминной задачи,
· произвольный план работы станков, число полных комплектов деталей для этого плана,
· преобразование математической модели к задаче линейного программирования с частично целочисленными переменными,
· оптимальный план работы станков, максимальное число полных комплектов,
· диаграмму, отражающую оптимальный план работы станков,
· выводы по работе.