Задание на работу. Древесно-стружечные плиты размером подлежат раскрою на детали двух типоразмеров: и

Древесно-стружечные плиты размером 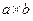подлежат раскрою на детали двух типоразмеров: 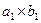и 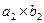. Требуется получить не менее 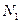деталей первого и не менее 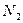деталей второго типоразмера. Определить наилучший план раскроя.

В такой постановке задача является некорректной, поскольку указанное число заготовок может быть получено многими способами и не понятно, какой из способов является более предпочтительным по отношению к другим. Для получения однозначного решения задачи введем следующие критерии оптимальности:

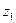– минимальное количество плит, затраченных на раскрой;

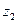– минимум суммарной площади отходов;

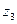– минимум суммарной длины пропилов; этот критерий может быть важен для экономии электроэнергии при работе станка.

Принятие наилучшего решения зависит от выбранного критерия оптимальности. Для решения данной задачи необходимо выполнить следующие пункты:

1. Разработать возможные варианты (карты) раскроя ДСтП.

2. Составить математическую модель в виде задачи линейного целочисленного программирования по критерию минимального расхода плит. Решить задачу в Excel.

3. Составить математическую модель в виде задачи линейного целочисленного программирования по критерию минимизации отходов. Решить задачу в Excel.

4. Составить математическую модель в виде задачи линейного целочисленного программирования по критерию минимума суммарной длины пропилов. Решить задачу в Excel.

5. Составить сравнительную таблицу с результатами оптимизации по трем критериям.

6. Показать результаты оптимизации на диаграмме.