
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическая модель максимизации прибыли
|
|
Фактическая загрузка по каждой группе оборудования равна: 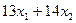 – для строгальных станков,
– для строгальных станков, 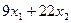 – для фрезерных станков,
– для фрезерных станков, 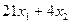 – для шлифовальных станков. Коэффициенты при неизвестных обозначают здесь нормы затрат машинного времени на обработку одного шкафа и одного стола. Загрузка по каждой группе оборудования не должна превышать фонда машинного времени, т.е.:
– для шлифовальных станков. Коэффициенты при неизвестных обозначают здесь нормы затрат машинного времени на обработку одного шкафа и одного стола. Загрузка по каждой группе оборудования не должна превышать фонда машинного времени, т.е.:
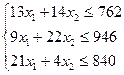 . (1.3)
. (1.3)
Неизвестные, очевидно, должны быть неотрицательными:
 ,
, 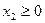 . (1.4)
. (1.4)
Неравенства (1.3) и (1.4) образуют систему ограничений. Общая прибыль от реализации готовой продукции (цель 1) выражается формулой
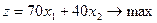 . (1.5)
. (1.5)
Таким образом, математическая модель задачи по критерию максимальной прибыли состоит в определении чисел 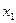 и
и 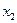 , удовлетворяющих системе ограничений (1.3)-(1.4), для которых значение функции (1.5) будет максимальным. Это есть задача линейной оптимизации.
, удовлетворяющих системе ограничений (1.3)-(1.4), для которых значение функции (1.5) будет максимальным. Это есть задача линейной оптимизации.