
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание на работу
|
|
Мебельная фабрика выпускает два вида изделий: шкафы и столы. В производстве применяется оборудование трех типов: фрезерные, сверлильные и шлифовальные станки. Нормы времени работы каждого вида оборудования в час, необходимые для изготовления одного изделия каждого вида, а также ресурсы рабочего времени для каждого вида оборудования, известны и приведены в табл. 1.1.
Т а б л и ц а 1.1
| Оборудование | Затраты машинного времени на обработку единицы продукции, ч | Эффектив-ный фонд времени станков, ч | Цена за простой единицы оборудования, ден.ед. | |
| Шкаф | Стол | |||
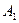 (фрезерные станки) (фрезерные станки)
| 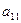
| 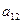
| 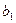
| 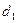
|
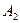 (сверлильные станки) (сверлильные станки)
| 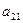
| 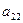
| 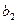
| 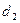
|
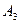 (шлифовальные станки) (шлифовальные станки)
| 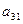
| 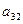
| 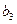
| 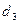
|
| Прибыль от реализации единицы продукции, ден.ед. | 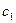
| 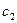
|
Фабрика получает прибыль от изготовления и реализации одного шкафа в размере 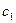 ден.ед. и одного стола – в размере
ден.ед. и одного стола – в размере 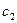 ден.ед. Цена за простой 1 часа оборудования
ден.ед. Цена за простой 1 часа оборудования 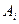 составляет
составляет 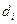 ден.ед.,
ден.ед., 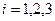 . Эти данные содержатся в таблице.
. Эти данные содержатся в таблице.
Требуется определить план выпуска изделий каждого вида, при котором время работы оборудования не превышало бы допустимого фонда времени, и при этом
· во-первых, была получена наибольшая общая прибыль;
· во-вторых, был получен минимальный штраф за простой оборудования;
· в третьих, была получена наибольшая общая прибыль с учетом штрафа за простой оборудования.
Для решения задачи необходимо выполнить следующие пункты:
1. Составить математическую модель задачи при условии, что критерием оптимальности является максимальная прибыль от изготовления и реализации продукции. Решить полученную задачу линейного программирования графически и с помощью процедуры «Поиск решения» программного средства Excel.
2. Составить математическую модель при условии, что критерием оптимальности является минимальный штраф за простой оборудования. Решить задачу в Excel.
3. Составить математическую модель при условии, что критерием оптимальности является максимум общей прибыли за вычетом штрафа за простой оборудования. Решить задачу в Excel.
4. Показать соответствие оптимальных планов с вершинами допустимой области.