
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая работа №10
|
|
«Статистическое распределение выборки средствами Mathcad»
Выполнив задания этой работы вы научитесь:
1. Строить вариационный ряд;
2. Различать различные статистические ряды;
3. Строить полигон частот для статистического ряда;
4. Строить гистограмму для группированного ряда.
Задание 1: Проведено n =10 измерений отклонения напряжения сети от номинального уровня. Полученные данные с точностью до вольта составляют следующую выборку: 0, -1, -3, 2, 1, 0, -1, -2, 1, -1. Сформировать вариационный, статистический и группированный ряды.
Технология выполнения задания:
1. Вариационным рядом называют совокупность всех элементов выборки, записанных в неубывающем порядке.
Прежде всего, необходимо сформировать данную выборку в виде матрицы-столбца (см. практ. раб. №4).
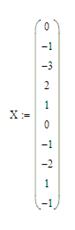
Для сортировки значений в порядке возрастания в Mathcad используется функция sort(). Пусть столбец X1 – столбец значений матрицы X, расположенных в указанном порядке. На рабочем листе набираем:
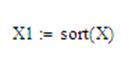
Ниже этой записи пишем X1 и ставим знак равенства «=», а не присваивания «: =». Выполнив эту операцию, получим:

Таким образом, вариационным рядом этой выборки служит последовательность: -3, -2, -1, -1, -1, 0, 0, 1, 1, 2.
При этом можно определить наименьший и наибольший член матрицы. Для этого на рабочем листе набираем min(X1) или max(X1), ставим знак «=» и получаем:

Таким образом, наименьшее значение выборки равно -3, а наибольшее – 2.
2. Статистическим рядом называют последовательность различных элементов выборки y1, y2, …, записанных в возрастающем порядке и частот n1, n2, …, с которыми эти элементы содержатся в выборке.
Статистический ряд с абсолютными частотами для исходной выборки будет иметь вид:
| yi | -3 | -2 | -1 | |||
| ni |
При решении прикладных задач часто используется статистический ряд, составленный для относительных частот wi = 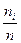 .
.
Тот же статистический ряд с относительными частотами примет вид:
| yi | -3 | -2 | -1 | |||
| wi | 0, 1 | 0, 1 | 0, 3 | 0, 2 | 0, 2 | 0, 1 |
Вопросы к размышлению: Почему подобную таблицу не формируют встроенные функции программы Mathcad? Попробуйте создать подпрограмму-функцию для решения этой задачи.
Для данной зависимости можно построить функцию, которая будет называться полигоном частот.
Для построения полигона частот зададим две матрицы y – состоящую из значений выборки и w – состоящую из относительных частот выпадения данного значения, далее вызвать двухмерную систему координат, забить промежутки по оси Ox [-4; 3], по оси Oy [0; 0, 4] и построить график (см. практ. раб. №4).

Для изменения вида линий в окне «Formatting Currently Selected X-Y Plot», выбрав закладку «Traces» в колонке «Simbol» выберем черный ромб:
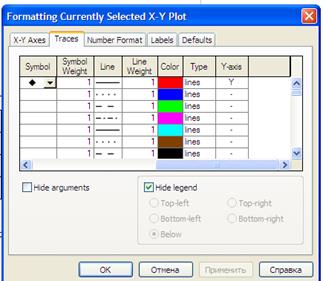
Нажав кнопку «Применить», получим полигон частот:
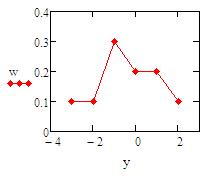
В практических задачах при объемных массивах данных статический ряд необходим гораздо реже, чем группированный статистический ряд.
Группированным статистическим рядом называют совокупность середин промежутков и соответствующих им частот попаданий значений в данный промежуток.
Наглядное представление о группированном статистическом ряде можно получить, составляя гистограмму.
Гистограммой называется график, аппроксимирующий по выборочным данным плотность эмпирического распределения. При построении гистограммы область наблюдаемых значений случайной величины разбивается на n равных интервалов и подсчитывается количество попаданий данных в каждый интервал. В Mathcad для построения гистограммы используется функция histogram(b, X).
Пусть данные о выборке составляют матрицу-столбец X, а X1 – столбец значений матрицы X, расположенных в порядке возрастания. Пусть число промежутков b будет равно 6. Тогда зададим матрицу F, первый столбец которой будет состоять из середин промежутков разбиения, а второй – из количества значений попавших в этот промежуток.
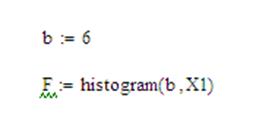
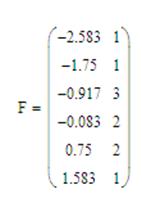
В двухмерной системе координат по оси Ox зададим промежуток [-4; 3] и расположим значения первого столбца матрицы F, по оси Oy на промежутке [0; 4] расположим значения второго столбца матрицы F. Выбрав в настройках линий вид линии «bar», получим гистограмму распределения.
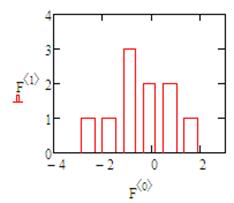
Внимание! В некоторых учебниках и специальной литературе гистограмма может иметь вид, приведенный ниже. Такой вид гистограммы тоже имеет место, т.к. связан с выбором другого типа линий (в данном случае «step»).
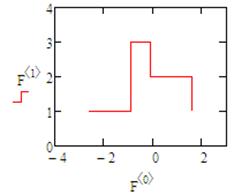
Вопросы к размышлению: Для каких целей в программе Mathcad предусмотрена еще одна встроенная функция для построения гистограмм hist(intervals, data)? Попробуйте построить гистограмму при помощи этой функции.
Задание для самостоятельного решения: В таблице приведены результаты неких наблюдений
| 4, 622 | 1, 259 | 0, 053 | 1, 903 | 0, 272 | 1, 087 | 0, 759 | 2, 113 | 3, 384 | 2, 617 |
| 2, 971 | 2, 724 | 2, 831 | 2, 346 | 1, 089 | 1, 138 | 0, 511 | 2, 393 | 0, 636 | 1, 289 |
| 0, 446 | 2, 033 | 2, 116 | 1, 151 | 1, 179 | 3, 824 | 0, 411 | 1, 604 | 3, 215 | 3, 785 |
| 1, 802 | 1, 37 | 3, 912 | 1, 923 | 1, 395 | 4, 198 | 2, 542 | 1, 612 | 1, 023 | 0, 529 |
| 1, 982 | 0, 348 | 0, 736 | 3, 036 | 1, 37 | 2, 027 | 2, 48 | 0, 967 | 1, 558 | 1, 324 |
Построить гистограмму относительных частот с 7 интервалами.