
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая работа №5. «Дискретная случайная величина»
|
|
«Дискретная случайная величина»
Выполнив задания этой работы вы научитесь:
1. Строить полигон распределения и функцию распределения вероятностей дискретной случайной величины;
2. Вычислять числовые характеристики дискретной случайной величины: математическое ожидание, дисперсию, среднеквадратичное отклонение.
Случайной величиной называется величина, которая в результате опыта может принять любое значение, причем заранее неизвестно – какое.
Дискретной случайной величиной называется случайная величина, принимающее конечное либо счетное множество значений, которые можно пронумеровать (например, число очков, выпавших при бросании игральной кости, есть дискретная величина).
Соотношение между возможными значениями дискретной случайной величины и соответствующими им вероятностями называется законом распределения дискретной случайной величины, который может быть записан в виде таблицы, аналитически или графически.
Табличный способ задания закона распределения:
| X | x1 | x2 | … | xi | … | xn |
| P | p1 | p2 | … | pi | … | pn |
Где X – значение случайной величины;
P – вероятности этих значений.
Функцией распределения F(x) случайной величины X называется вероятность того, что случайная величина примет значение, меньшее x: F(x)=P(X< x).
Функция распределения дискретной случайной величины, имеющей приведенное выше распределение, имеет вид:
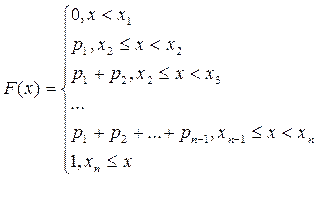
Для наглядности закон распределения дискретной случайной величины изображают графически: для этого в прямоугольной системе координат по оси Ox откладывают значения случайной величины, по оси Oy – вероятности этих значений, наносят точки (xi, pi), i=1, …, n, и, соединяют их последовательно отрезками прямой. Получающаяся при этом ломаная линия называется полигоном (многоугольником) распределения случайной величины X.
Вероятность того, что случайная величина попадает в интервал[a; b] выражается по формуле: P(a≤ X≤ b)= 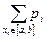 .
.
Числовые характеристики дискретной случайной величины:
· Математическое ожидание показывает абсциссу центра тяжести распределения «масс вероятности».
Математическое ожидание M(x): M(X)= 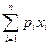 ;
;
· Дисперсия D(x): D(X)= 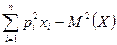 ;
;
· Среднеквадратичное отклонение: σ (X)= 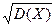 .
.
Задание1: Случайная дискретная величина X задана распределением:
| X | -1 | |||||
| P | 0.15 | 0.1 | 0.15 | 0.25 | 0.16 | 0.19 |
Построить полигон распределения вероятностей, функцию распределения, вычислить математическое ожидание, дисперсию, среднеквадратичное отклонение. Определить вероятность событий P(X< 0), P(X≥ 2), P(0≤ X≤ 4).
Технология выполнения задания: 1. Введем исходные данные (см. практ. раб. №4), в связи с тем, что Mathcad работает с матрицей-столбцом, лучше ввести матрицы следующим образом:

Зададим значение i – количество строк матрицы, используя функцию length(v), указывающей число элементов в векторе. Учтем, что Mathcad начинает считать с нулевой строки и нулевого столбца:
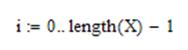
Условием для P зададим сумму всех значений матрицы P, равную 1:
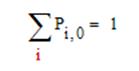
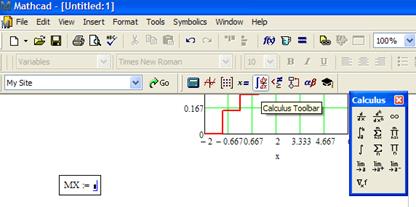
В декартовой системе координат отложим по оси Ox значения матрицы X, а по оси Oy – соответствующие им значения матрицы P:
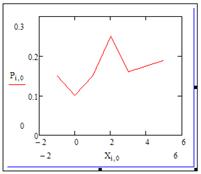
Для улучшения качества рисунка выполним следующие действия:
В закладке «X-Y Axes» произвести указанные изменения:
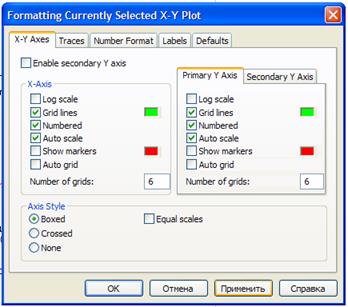
Нажав кнопку «Применить», получим:
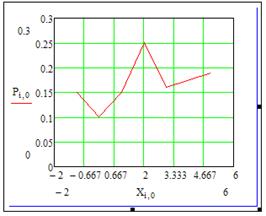
В закладке «Traces» внесем следующие изменения:
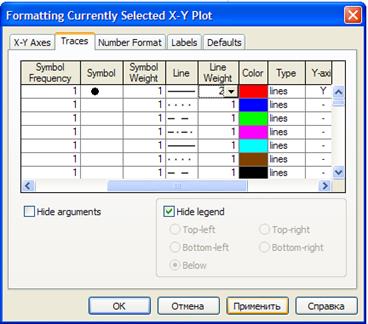
Нажав кнопку «Применить», получим:
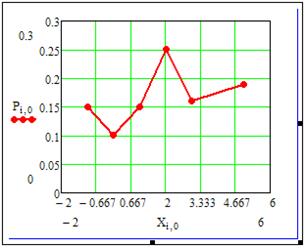
2. Построим функцию распределения и ее график. Функция распределения является функцией-подпрограммой (практ. раб. №9).
Сделаем заготовку для создания подпрограммы. Количество строчек должно быть на единицу больше, чем количество элементов в матрице X.
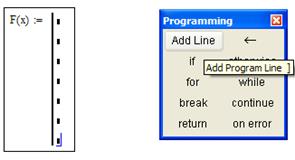
С помощью функций меню «Programming», а также меню для введения математических знаков «Boolean» введем функцию F(x):

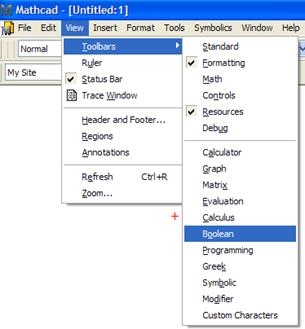
Для вызова функции «Boolean» выполним следующие действия:
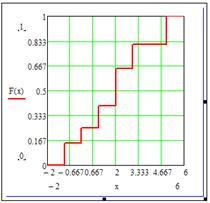
Построив сетку и сделав линию функции толще, получим:
Вычислим характеристики случайной величины:
Для этого настроим панель инструментов поставив значки напротив каждого из названий:
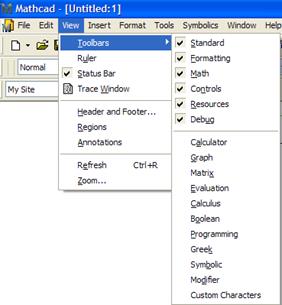
В результате получим:

· Математическое ожидание MX:
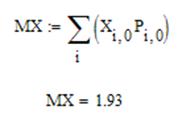
· Дисперсия DX:
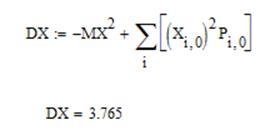
· Среднеквадратичное отклонение: σ X:
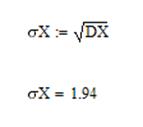
Для того, чтобы напечатать σ, выберем значок «Greek Symbol Toolbar» на панели инструментов:
Появится окно «Greek»:

Чтобы ввести квадратный корень выберем кнопку «Calculator Toolbar» на панели инструментов:
Появится окно «Calculator». Выбирая значок квадратного корня, набираем его значение.
3. Вычислим вероятность того, что случайная величина попадает в заданный интервал:

Задания для самостоятельного решения: 1. Дискретная величина X задана распределением вида x1 =0; x2 =1; p1 =q; p2 =p. Определить математическое ожидание и дисперсию.
2. Дискретная величина X задана распределением приведенным в таблице:
| x1 =0, 4 | x2 =6 | x3 |
| p1 =0, 5 | p2 =0, 3 | p3 |
Также известно математическое ожидание M(x)=8. Определить x3 и p3.