
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая работа №7. «Функции распределения вероятностей дискретной случайной величины»
|
|
«Функции распределения вероятностей дискретной случайной величины»
Выполнив задания этой работы вы научитесь:
1. Визуально определять вид распределения;
2. Строить графики распределения и функции распределения вероятности дискретной случайной величины;
3. Импортировать различную информацию в документ Mathcad.
1. Биномиальный закон распределения.
Случайная величина Х, которая принимает значение с вероятностью
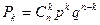 , где p – вероятность успеха в одном испытании, 0≤ p ≤ 1, называется распределенной по биномиальному закону.
, где p – вероятность успеха в одном испытании, 0≤ p ≤ 1, называется распределенной по биномиальному закону.
Для вычисления вероятностей Pk и функции распределения F(k) случайной величины X предназначены функции:
dbinom(k, n, p) – выводит значение вероятностей;
pbinom(k, n, p) – выводит значение кумулятивных вероятностей.
Пример 1. Пусть n =15, а p =0, 2. Построить графики распределения вероятностей при помощи обоих операторов.
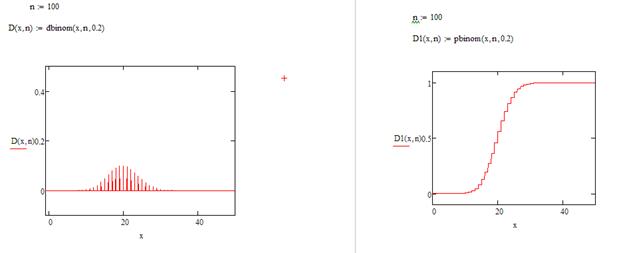
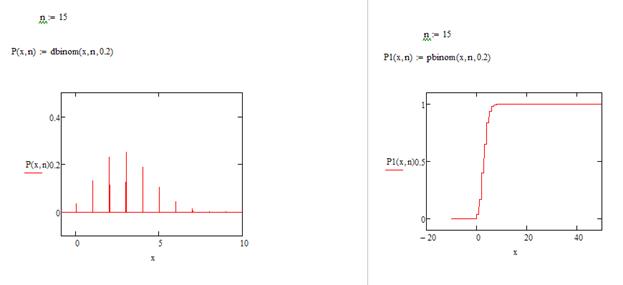
Задание: 1. Рассмотрите графики. Чем график коммулятивной вероятности отличается от графика распределения вероятности?
1. Определите по графику значение математического ожидания при различных значениях n. Подтвердите свои предположения вычислениями.
2. Распределение Пуассона.
В данном распределении случайная величина X принимает значения k с вероятностью 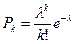 , где λ – математическое ожидание.
, где λ – математическое ожидание.
Для вычисления вероятностей Pk и функции распределения F(k) случайной величины X предназначены функции:
dpois(k, λ) – выводит значение вероятностей;
ppois(k, λ) – выводит значение кумулятивных вероятностей.
Пример 2. Пусть λ =5. Построить графики распределения вероятностей при помощи обоих операторов, если вы хотите проверить вероятность выпадение одиннадцати значений от 0 до 10.
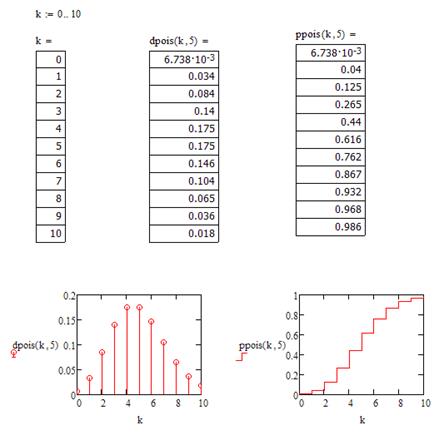
Задание: 1. Измените значения k и значение математического ожидания. Как при этом изменятся графики?
3. Геометрическое распределение.
В данном распределении случайная величина X принимает значение k с вероятностью 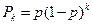 , где p – вероятность успеха, 0≤ p ≤ 1, k=0, 1, 2, …
, где p – вероятность успеха, 0≤ p ≤ 1, k=0, 1, 2, …
Для вычисления вероятностей Pk и функции распределения F(k) случайной величины X предназначены функции:
dgeom(k, p) – выводит значение вероятностей;
pgeom(k, p)– выводит значение кумулятивных вероятностей.
Пример 2. Пусть p =0, 4. Построить графики распределения вероятностей при помощи обоих операторов, если вы хотите проверить вероятность выпадение одиннадцати значений от 0 до 10.
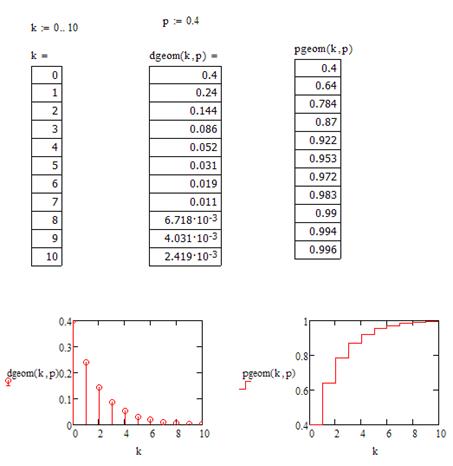
Задание: 1. Измените значения k и p. Как при этом изменятся графики?
Задания для самостоятельного выполнения:
1. Найти при помощи учебников, Internet или других источников информацию о том, какие еще бывают законы распределения дискретной случайной величины.
2. Какой вид имеют эти распределения.
3. Импортировать картинки с их графическим представлением в документ Mathcad.