
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 10. Найти наибольшее и наименьшее значение функции в замкнутом треугольнике АОВ, ограниченном осями координат и прямой (рис
|
|
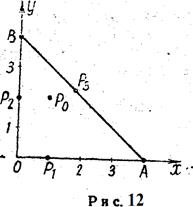
Найти наибольшее и наименьшее значение функции  в замкнутом треугольнике АОВ, ограниченном осями координат и прямой
в замкнутом треугольнике АОВ, ограниченном осями координат и прямой 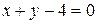 (рис. 12).
(рис. 12).
Решение. Найдем стационарные точки.
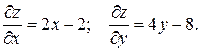
Решая систему
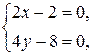
находим стационарную точку  . Эта точка лежит внутри области. Вычислим значение функции в этой точке.
. Эта точка лежит внутри области. Вычислим значение функции в этой точке.
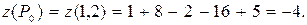
Граница заданной области состоит из отрезка О А оси Ох, отрезка ОВ оси Оу и отрезка АВ. Определим наибольшее и наименьшее значение функции 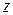 на каждом из этих трех участков. На отрезке ОА
на каждом из этих трех участков. На отрезке ОА 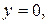 а
а  . При
. При 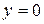 функция
функция 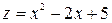 есть функция одной независимой переменной х. Находим наибольшее и наименьшее значение этой функции на отрезке
есть функция одной независимой переменной х. Находим наибольшее и наименьшее значение этой функции на отрезке 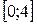 .
.
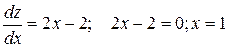 ;
; 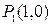 – стационарная точка.
– стационарная точка. 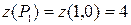 .
.
Вычислим значения функции на концах отрезка ОА, то есть в точках О и А. 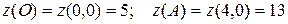 .
.
На отрезке ОВ 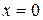 и
и 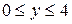 . При
. При 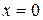 имеем
имеем 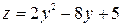 . Находим наибольшее и наименьшее значение этой функции
. Находим наибольшее и наименьшее значение этой функции 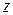 от переменной у на отрезке
от переменной у на отрезке 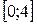 .
. 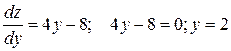 ;
; 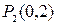 – стационарная точка.
– стационарная точка.  .
.
Вычислим значения функции  на концах отрезка ОВ, то есть в точках О и В.
на концах отрезка ОВ, то есть в точках О и В. 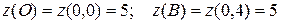 . Исследуем теперь отрезок АВ. Уравнение прямой АВ:
. Исследуем теперь отрезок АВ. Уравнение прямой АВ: 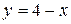 . Подставив это выражение для у в заданную функцию
. Подставив это выражение для у в заданную функцию 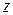 , получим
, получим 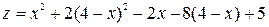 или
или 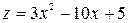 . Определим наибольшее и наименьшее значение этой функции на отрезке
. Определим наибольшее и наименьшее значение этой функции на отрезке 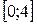 .
.
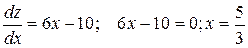 ;
; 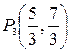 – стационарная точка.
– стационарная точка. 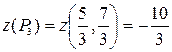 .
.
Значения функции в точках А и В найдены ранее. Сравнивая полученные результаты, заключаем, что наибольшее значение заданная функция 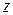 в заданной замкнутой области достигает в точке
в заданной замкнутой области достигает в точке 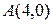 , а наименьшее значение – в стационарной точке
, а наименьшее значение – в стационарной точке  . Таким образом,
. Таким образом,
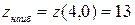 и
и 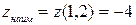 .
.
Вопросы для подготовки