Функции многих переменных

1. Понятие функции двух переменных 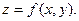Геометрическое истолкование. Область определения.

2. Линии уровня, их графическая интерпретация и применение. Исследование линий уровня функции .

3. Предел и непрерывность функции нескольких переменных.

4. Свойства функций, непрерывных в ограниченной замкнутой области.

5. Определение и геометрический смысл частных производных.

6. Частные производные высших порядков. Теорема о независимости смешанных производных от порядка дифференцирования.

7. Дифференцирование сложной функции 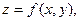где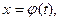

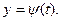
8. Понятие полной производной.

9. Дифференцирование сложной функции 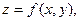где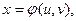

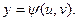
10. Касательная плоскость и нормаль к поверхности, определяемой графиком функции двух переменных.

11. Производная по направлению. Определение, связь с частными производными. Вывод формулы для нахождения.

12. Градиент функции, его связь с производной по направлению.

13. Определение и геометрический смысл полного дифференциала функции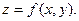

14. Дифференцируемость функции нескольких переменных. Свойства дифференцируемой функции: непрерывность, существование частных производных.

15. Достаточные условия дифференцируемости функции двух переменных.

16. Применение полного дифференциала к приближенным вычислениям.

17. Инвариантность формы и другие свойства полного дифференциала.

18. Дифференциалы высших порядков.

19. Неявные функции и их дифференцирование.

20. Уравнение касательной к кривой, задаваемой неявной функцией.

21. Определение точек экстремума функции 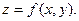Необходимые и достаточные условия экстремума.

22. Выпуклые множества и выпуклые функции. Особенности экстремума для выпуклых функций. Глобальный экстремум. Нахождение наибольшего и наименьшего значения функции в области.

23. Условный экстремум. Функция Лагранжа.

24. Общая теория функции двух переменных на примере ПФ Кобба-Дугласа. (Область определения, график, линии уровня, частные производные и их экономическая интерпретация, эластичность, предельная норма замены, закон убывающей эффективности).

25. Функция полезности. Задача потребительского выбора. (Понятие полезности, бюджетное множество, функция полезности, ее линии уровня, частные производные и их экономическая интерпретация, закон убывающей полезности, предельная норма замены, задача потребительского выбора и ее решение, точка спроса и ее характеристика).

Литература

а) основная литература

1. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. –М.: Юрайт, 2010.-646с.

2. Рождественский К.Н. Математика.: Рабочая тетрадь. / ИЗУ ВПА.-Тула: Папирус, 2012.- 48с.

б) дополнительная литература

3. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. Ч. 1 и 2.- М.: Высшая школа, 1982.

4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1989.

5. Четыркин Е.М. Методы финансовых и коммерческих расчетов. — М.: «Дело Лтд», 1995 г. — 320 с.

6. Берман Г. Н. Сборник задач по курсу математического анализа. М., Наука, 1985.

7. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М., Наука, 1988.

8. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1. М.., Высшая школа, 1980.

9. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. 1. М., Наука, 1976.

10. Сборник задач по математике для втузов. В 4-х частях. Ч. 1. Линейная алгебра и основы математического анализа. Под ред. А.В. Ефимова, Б.П. Демидовича. М., Наука, 1993.

[1] Рекомендуем сдавать работу на проверку несколько раньше, т.к. в случае отрицательной рецензии на переработку контрольной работы потребуется дополнительное время, приходящее на экзаменационную сессию. Напоминаем, что студент, не получивший зачет по данной работе, к экзамену допущен не будет.