
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельного решения. 1. На трех линиях инкубатора заложены яйца в пропорции 1:2:3
|
|
1. На трех линиях инкубатора заложены яйца в пропорции 1: 2: 3. В результате случайного повышения температуры в инкубаторе на первой линии погибли 10% зародышей, на второй – 5%, на третьей – 20%. Какова вероятность того, что зародыш в наудачу взятом яйце не погиб?
2. Литье в болванках поступает из двух заготовительных цехов: 75% из первого и 25% из второго. При этом материал первого цеха имеет 15% брака, а второго – 20%. Взятая наугад болванка оказалась стандартной. Найти вероятность того, что она была изготовлена первым цехом.
3. В первом ящике содержится 20 деталей, из них 15 стандартных. Во втором ящике 30 деталей, из них 24 стандартных. Из первого ящика перекладывают деталь во второй. Найти вероятность того, что случайным образом извлеченная деталь из второго ящика стандартная.
4. Вся продукция проверяется двумя контролерами. Вероятность того, что изделие попадет на проверку к первому контролеру, равна 0, 55, а ко второму – 0, 45. Вероятность того, что первый контролер обнаружит нестандартное изделие, равна 0, 91, а для второго – 0, 98. Какова вероятность, что выбранное изделие нестандартно?
5. Калийное удобрение поступает на склад хозяйства с завода 1 и с завода 2, причем с 1-го завода в 3 раза больше, чем со второго. Вероятность того, что удобрение с 1-го завода удовлетворяет стандарту 0, 8; со второго завода - 0, 7. Определить вероятность того, что взятое для пробы удобрение удовлетворяет стандарту.
6. В трех клетках находятся мыши. В первой клетке 15% мышей заболело вирусной инфекцией, во второй – 10%, в третьей – 20%. Из наудачу взятой клетки берут одну мышь. Какова вероятность того, что эта мышь здорова?
7. В двух корзинках находятся грибы: в первой 12 шт., из которых 4 белых, во второй 24 шт., из которых 6 белых. Из наудачу выбранной корзинки взяли гриб. Какова вероятность того, что он белый?
8. Навоз транспортируется на поля хозяйства из пункта А и пункта В, из первого пункта в 2 раза меньше, чем из второго. В первом пункте 80% перегнившего навоза, во втором – 90%. Взятый для пробы на поле навоз оказался перегнившим. Какова вероятность того, что он был завезен из пункта В?
9. Для посадки заготовлены три сорта семян бобов, из них первого сорта – 60%, второго – 10%, третьего – 30%, Вероятность того, что длина стручка не превышает 17 см, для первого сорта равна 0, 75, для второго – 0, 1, для третьего 0, 15. Какова вероятность того, что взятый наудачу стручок имеет длину не менее 17 см?
10. На склад поступает продукция трех фирм. Продукция первой фирмы составляет 25 % всей продукции, второй – 45%, третьей – 30%. Средний процент бракованной продукции для первой фирмы равен 2%, для второ1 – 1%, для третьей – 1, 5%. Взятая наудачу продукция оказалась бракованной. Какова вероятность того, что она была произведена второй фирмой?
11. На фермах А и В произошла вспышка заболевания туберкулезом. Доли зараженного скота составляют соответственно 60% и 40%. Какова вероятность того, что случайным образом отобранное для обследования животное оказалось больным?
12. Имеется две клетки. В первой 4 белых и 6 черных, во второй 6 белых и 8 черных кроликов. Из первой клетки во вторую перекладывают, не глядя, одного кролика. После этого из второй клетки берут одного кролика. Найти вероятность того, что этот кролик будет черным.
13. В партии 40% яблок собраны на первом участке и 60% на втором. Вероятность того, что с первого участка яблоки стандартные 90%, со второго – 80%. Взятое наудачу яблоко оказалось нестандартным. Найти вероятность того, что оно было собрано на втором участке.
14. На сортоиспытательной станции при подготовке семян к посеву основную их массу подвергают различным воздействиям: 75% облучают в электромагнитном поле, а остальные семена протравливают в химическом растворе. Облученные семена прорастают с вероятностью 0, 9, протравленные – с вероятностью 0, 8. какова вероятность того, что взятое наудачу семя прорастет?
15. Больного обследуют на одно из трех заболеваний: X, Y, Z. Вероятности заболевания соответственно равны 0, 5, 0, 2 и 0, 3. Для уточнения диагноза назначен некоторый тест. Тест не идеален и оказывается положительным лишь с некоторой вероятностью: если это X, то он положителен с вероятностью 0, 1; если Y – с вероятностью 0, 2; если же Z – то с вероятностью 0, 9. Требуется определить вероятность заболевания.
16. Установлено, что в данном русском тексте после гласной буквы стоит гласная с вероятностью 0, 15, а после согласной - согласная с вероятностью 0, 3. Найти вероятность того, что в наудачу выбранном слове, начинающемся с гласной буквы, третья буква будет гласной (В русском языке 10 гласных и 20 согласных).
17. Одноразовые шприцы поступают на сборку с трех автоматических линий: с первой линии поступает 40%, сов торой – 35%, с третьей – 25%. Среди шприцов, поступивших с первой линии, брак составляет 0, 2%, со второй – 0, 3%, с третьей – 0, 1%. Выбранный для проверки шприц оказался бракованным. Найти вероятность того, что он поступил со второй линии.
18. В первой урне 2 белых, 3 красных и 20 черных шаров, во второй – 5 белых, 2 красных и 3 черных шара. Какова вероятность того, что из наудачу выбранной урны извлечен черный шар?
19. В первой урне 2 белых, 3 красных и 20 черных шаров, во второй урне 5 белых, 2 красных и 3 черных шара. Из первой урны переложили шар во вторую. Какова вероятность извлечь из второй урны белый шар?
20. В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго – 10%, третьего – 5%. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30% телевизоров с первого завода, 20% - со второго и 50% - с третьего?
21. Из 10 студентов, пришедших сдавать экзамен по теории вероятностей взявших билеты, двое студентов знают 20 билетов из 30, трое студентов успели повторить только 15 билетов, остальные знают все 30 билетов. Знание билета гарантирует сдачу экзамена с вероятностью 0, 85, а при незнании билета – с вероятностью 0, 1. Какова вероятность того, что вызванный случайным образом студент сдал экзамен?
22. Из заготовленной для посева пшеницы зерно первого сорта составляет 50%, второго сорта – 30%, третьего сорта – 20%. Вероятность того, что взойдет зерно первого сорта, равна 0, 8, второго – 0, 6, третьего – 0, 4. выбранное наудачу зерно взошло. Какова вероятность того, что оно было первого сорта?
23. Имеются две партии изделий по 12 и 10 штук, причем в каждой партии одно изделие бракованное. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.
24. Для контроля продукции из трех одинаковых партий деталей взята для испытания одна деталь. Какова вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других все доброкачественные?
25. Радиолампа может принадлежать к одной из трех партий с вероятностями 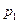 ,
, 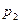 и
и 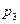 , где
, где 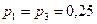 ,
, 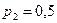 . Вероятности того, что лампа проработает заданное число часов, равны для этих партий соответственно 0, 1; 0, 2 и 0, 4. Определить вероятность того, что лампа проработает заданное число часов.
. Вероятности того, что лампа проработает заданное число часов, равны для этих партий соответственно 0, 1; 0, 2 и 0, 4. Определить вероятность того, что лампа проработает заданное число часов.
26. Характеристика материала, взятого для изготовления продукции, с вероятностями 0, 09; 0, 16; 0, 25; 0, 25; 0, 16 и 0, 09 может находиться в шести различных интервалах. В зависимости от свойств материала вероятности получения первосортной продукции равны соответственно 0, 2; 0, 3; 0, 4; 0, 4; 0, 3 и 0, 2. Определить вероятность получения первосортной продукции.
27. Телеграфное сообщение состоит из сигналов «точка» и «тире». Статистические свойства помех таковы, что искажаются в среднем 2/5 сообщений «точка» и 1/3 сообщений «тире». Известно, что среди передаваемых сигналов «точка» и «тире» встречаются в отношении 5: 3. Определить вероятность того, что был передан сигнал «точка», если принят сигнал «точка».
28. Имеется две партии деталей, причем известно, что в одной партии все детали удовлетворяют техническим условиям, а в другой партии ¼ деталей недоброкачественные. Деталь, взятая из наудачу выбранной партии, оказалась доброкачественной. Определить вероятность того, что она была взята из второй партии.
29. Имеется десять одинаковых урн, из которых в девяти находятся по два черных и по два белых шара, а в одной – пять белых и один черный шар. Из урны, взятой наудачу, извлечен белый шар. Какова вероятность, что шар извлечен из урны, содержащей пять белых шаров?
30. Известно, что 96% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0, 98 и нестандартную – с вероятностью 0, 05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
31. В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго - 10% и третьего-5%. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30 % телевизоров с первого завода, 20 % - со второго и 50 % - с третьего?
32. В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 игранных. Дня игры наудачу выбирают два мяча и после игры возвращают обратно. Затем для второй игры наудачу извлекаются еще два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?
33. Три стрелка, вероятности попадания для которых при одном выстреле в мишень соответственно равны 0, 8; 0, 7 и 0, 6, делают по одному выстрелу. Найти вероятность того, что в мишени окажется ровно две пробоины?
34. В первой урне 6 белых и 4 черных шара, во второй - 3 белых и 2 черных шара. Из первой урны наудачу извлекают три шара, и шары того цвета, которые окажутся в большинстве, опускают во вторую урну и тщательно перемешивают. После этого из второй урны наудачу извлекают один шар. Какова вероятность того, что этот шар белый?
35. 0пределить вероятность того, что 100 лампочек, взятых наудачу из 1000, окажутся исправными, если известно, что число испорченных лампочек на 1000 штук равновозможно от 0 до 5.
36. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму для лыжника - 0, 9; для велосипедиста - 0, 8; для бегуна - 0, 75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
37. В первой урне 4 белых и 2 черных шара; во второй 2 белых и 3 черных шара; в третьей 4 белых и 4 черных шара. Из первой и второй урн не глядя перекладывают по одному шару в третью урну. Шары в третьей урне перемешивают и из нее берут наугад один шар. Найти вероятность того, что этот шар белый.
38. В группе стрелков шесть отличных, девять хороших, восемь посредственных два плохих. Вероятности попадания в цель для них соответственно-равны: 0, 9; 0, 8; 0, 5; 0, 1. Наугад из группы вызывается один стрелок. Найти вероятность того, что он попадет в цель.
39. Имеются 5 акций предприятия А, 7 – предприятия В и 3 – предприятия С. Вероятность повышения акции А равна 0, 7, для В – 0, 5, для С – 0, 8. Какая вероятность, что случайно выбранная акция повысится в цене?
40. В первом ящике 6 белых и 4 черных шара, во втором - 7 белых и 3 черных. Из каждого ящика наугад вынимают по одному шару. Чему равна вероятность того, что вынутые шары разного цвета?
41. На двух станках производятся одинаковые детали. Вероятность того, что деталь стандартная, для первого станка равна 0, 8, для второго - 0, 9. Производительность второго станка втрое больше, чем первого. Найти вероятность того, что взятая наудачу деталь окажется стандартной.
42. На пяти карточках написано по одной цифре из набора: 1, 2, 3, 4, 5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой?
43. Телевизор может принадлежать к одной из трех партий с вероятностями 0, 25; 0, 5; 0, 25. Вероятности того, что телевизор проработает гарантийный срок без поломок, для этих партий равны соответственно 0, 1; 0, 2 и 0, 4. Определить вероятность того, что случайно выбранный телевизор проработает гарантийный срок.
44. В корзине 3 шара, каждый из которых с равной вероятностью может быть как белым, так и черным. Из корзины извлекли 1 шар. Он оказался белым. Какая вероятность, что в корзине осталось 2 черных шара?
45. Из полного набора костей домино наугад берутся две кости. Определить вероятность того, что вторую кость можно приставить к первой.
46. В двух урнах находится соответственно 4и 5 белых и 6и 3 черных шаров. Из каждой урны наудачу извлекается один шар, а затем из этих двух шаров наудачу берется один. Какова вероятность, что этот шар белый?
47. Имеется 3урны, в каждой из которых по 3белых и по 4 черных шаров. Из первой урны наудачу извлекается один шар и перекладывается во вторую. Затем из второй урны наудачу извлекается один шар и перекладывается в третью урну. Определить вероятность извлечения после такого перекладывания белого шара из последней урны.
48. В тире имеются пять ружей, вероятности попадания из которых равны соответственно 0, 5; 0, 6; 0, 7; 0, 8 и 0, 9. Определить вероятность попадания при одном выстреле, если стреляющий берет одно из ружей наудачу.
49. Для контроля продукции из трех партий деталей взята для испытания одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других — все доброкачественные?
50. Радиолампа может принадлежать к одной из трех партий с вероятностями 0, 3, 0, 4 и 0, 3. Вероятности того, что лампа проработает заданное число часов, равны для этих партий соответственно 0, 1; 0, 2 и 0, 4. Определить вероятность того, что случайно выбранная лампа проработает заданное число часов.
51. Игрок А играет поочередно с двумя партнерами, вероятности выигрыша для которых в первой партии равны соответственно 0, 5 и 0, 6 и увеличиваются после каждой сыгранной партии на 0, 1. Определить вероятность проигрыша А в третьей партии, если неизвестно, с каким партнером была сыграна первая партия, а ничьи исключены.
52. В левом кармане 5 монет по 1 рублю и 3 по 2 рубля, а в правом 3 монеты по 1 рублю и 4 по 2 рубля. Из левого кармана в правый наудачу переложили 2 монеты, перемешали, и из правого кармана извлекли монету. Какая вероятность, что это 2 рубля?
53. В группе студентов из 25 человек, пришедших сдавать экзамен, 10 подготовлены отлично, 7 - хорошо, 5 - удовлетворительно и 3 - плохо. Подготовленные отлично знают ответы на все 25 вопросов программы; хорошо - на 20; удовлетворительно - на 15; плохо - на 10 вопросов. Вызванный наудачу студент ответил на два заданных вопроса. Найти вероятность того, что этот студент плохо подготовлен к экзамену.
54. Шесть шаров, среди которых 3 белых и три черных, распределены по двум урнам. Наудачу выбирается урна, а из нее один шар. Как нужно распределить шары по урнам, чтобы вероятность вынуть белый шар была максимальна?
55. Два стрелка поочередно стреляют в мишень. Вероятности попадания первыми выстрелами для них равны соответственно 0, 4 и 0, 5, а вероятности попадания при последующих выстрелах для каждого увеличиваются на 0, 05. Найти вероятность того, что первым произвел выстрел первый стрелок, если при пятом выстреле произошло попадание в мишень.
56. Один из четырех стрелков вызывается на линию огня и производит выстрел по мишени. Вероятности попадания в мишень при одном выстреле для стрелков соответственно равны 0, 2; 0, 5; 0, 7; 0, 9. Мишень поражена. Найти вероятность того, что выстрел произведен четвертым стрелком.
57. Для участия в студенческих отборочных спортивных соревнованиях выделены из первой группы курса 4, из второй - 6, из третьей - 5 студентов. Вероятности того, что студент первой, второй и третьей групп попадет в сборную команду института, соответственно равны 0, 9; 0, 7; 0, 8. Наудачу выбранный студент в итоге соревнований попал в сборную института. Из какой группы вероятнее всего этот студент?
58. Имеется десять одинаковых урн, из которых в девяти находятся по два черных и по два белых шара, а в одной пять белых и один черный шар. Из урны, взятой наудачу, извлечен белый шар. Какова вероятность, что шар извлечен из урны, содержащей пять белых шаров?
59. Известно, что 96% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0, 98 и нестандартную - с вероятностью 0, 05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
60. Из 18 стрелков 5 попадают в мишень с вероятностью 0, 8; 7 — с вероятностью 0, 7; 4 — с вероятностью 0, 6 и 2 — с вероятностью 0, 5. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. К какой из групп вероятнее всего принадлежал этот стрелок?
61. Вероятности попадания при каждом выстреле для трех стрелков равны соответственно 4/5, 3/4, 2/3. При одновременном выстреле всех трех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок.
62. В связке 5 разных ключей, и один из них соответствующей двери. Делается попытка открыть наудачу взятым колючем, ключ неподходящий более не используется. Найти вероятность того, что а) дверь будет открыта 1-ым ключом; Б) Для открытия двери будет использовано не более двух ключей.
63. Трое охотников одновременно выстрелили по кабану, который был убит одной пулей. Определить вероятности того, что кабан убит первым, вторым или третьим охотником, если вероятности попадания для них равны соответственно 0, 2; 0, 4; 0, 6.
64. Попадание случайной точки в любое место области А равновозможно, а область А состоит из четырех частей, составляющих соответственно 50, 30, 12 и 8 % всей области. При испытании имело место событие В, которое происходит только при попадании случайной точки в каждую из этих частей с вероятностями соответственно 0, 01, 0, 05, 0, 2 и 0, 5. В какую из частей области А вероятнее всего произошло попадание?
65. Из двух близнецов первый — мальчик. Какова вероятность, что другой тоже мальчик, если среди близнецов вероятность рождения двух мальчиков и двух девочек соответственно равны 0, 4и 0, 4, а для разнополых близнецов вероятность родиться первым для обоих полов одинакова?
66. Принимая, что вероятность рождения однополых близнецов вдвое больше, чем разнополых, вероятности рождения близнецов разного пола в любой последовательности одинаковыми, а вероятность рождения мальчика равной 0, 51. девочки — 0, 49, определить вероятность рождения второго мальчика, если первым родился мальчик.
67. Два стрелка поочередно стреляют в мишень. Вероятности попадания первыми выстрелами для них равны соответственно 0, 4 и 0, 5, а вероятности попадания при последующих выстрелах для каждого увеличиваются на 0, 05. Какова вероятность, что первым произвел выстрел первый стрелок, если при третьем выстреле произошло попадание в мишень?
68. Третья часть одной из трех партий деталей является второсортной, остальные детали первого сорта. Деталь, взятая из одной партии, оказалась первосортной. Определить вероятность того, что деталь была взята из партии, имеющей второсортные детали.
69. Получена партия из восьми изделий одного образца. По данным проверки половины партии, три изделия оказались технически исправными, а одно бракованным. Какова вероятность того, что при проверке трех последующих изделий одно из них окажется исправным, а два бракованными, если любое количество бракованных изделий в данной партии равновозможно?
70. Из партии в четыре изделия наудачу взято одно изделие, оказавшееся бракованным. Количество бракованных изделий равновозможно любое. Какое предположение о количестве бракованных изделий наиболее вероятно?