
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельного решения. 1. В первом ящике 2 белых и 10 черных шаров; во втором ящике 8 белых и 4 черных шара
|
|
1. В первом ящике 2 белых и 10 черных шаров; во втором ящике 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые?
2. В первом ящике 2 белых и 10 черных шаров; во втором ящике 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Какова вероятность, что один шар белый, а другой черный?
3. В ящике 6 белых и 8 черных шаров. Из ящика вынули два шара (не возвращая вынутый шар в ящик). Найти вероятность того, что оба шара белые.
4. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0, 75, для второго – 0, 8, для третьего – 0, 9. Определить вероятность того, что все три стрелка одновременно попадут в цель; в цель попадет хотя бы один стрелок.
5. В урне 9 белых и 1 черный шар. Вынули сразу три шара. Какова вероятность того, что все шары белые?
6. Производят три выстрела по одной мишени. Вероятность попадания при каждом выстреле равна 0, 5. Найти вероятность того, что в результате этих выстрелов произойдет только одно попадание.
7. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0, 7 и 0, 8, производят по одному выстрелу. Определить вероятность хотя бы одного попадания в мишень.
8. Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0, 7, При изготовлении такой же детали на втором станке эта вероятность равна 0, 8. На первом станке изготовлены две детали, на втором три. Найти вероятность того, что все детали первосортные.
9. Работа прибора прекратилась вследствие выхода из строя одной лампы из пяти. Отыскание этой лампы производится путем поочередной замены каждой лампы новой. Определить вероятность того, что придется проверять 2 лампы, если вероятность выхода из строя каждой лампы равна р=0, 2.
10. На участке АВ для мотоциклиста-гонщика имеются 12 препятствий, вероятность остановки на каждом из которых равна 0, 1. Вероятность того, что от пункта В до конечного пункта С мотоциклист проедет без остановки, равна 0, 7. Определить вероятность того, что на участке АС не будет ни одной остановки.
11. На пути автомобиля 4 светофора. Вероятность остановиться на первых двух 0, 3, а на последующих двух 0, 4. Какая вероятность проехать светофоры без остановок?
12. На пути автомобиля 3 светофора. Вероятность остановиться на первых двух 0, 4, а на третьем 0, 5. Какая вероятность проехать светофоры с одной остановкой?
13. Два сервера сети в Интернет подвергаются опасности вирусной атаки за сутки с вероятностью 0, 3. Какая вероятность, что за 2 суток на них не было ни одной атаки?
14. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 2/3, Если при первом выстреле зафиксировано попадание, то стрелок получает право на второй. Если при втором он вновь попадет, то стреляет третий раз. Какая вероятность попасть при трех выстрелах?
15. Игра между А и В ведется на следующих условиях: в результате первого хода, который всегда делает А, он может выиграть с вероятностью 0, 3; если первым ходом А не выигрывает, то ход делает В и может выиграть с вероятностью 0, 5; если в результате этого хода В не выигрывает, то А делает второй ход, который может привести к его выигрышу с вероятностью 0, 4. Определить вероятности выигрыша для А и для В.
16. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна 0, 2. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки.
17. Игрок А поочередно играет по две партии с игроками В и С. Вероятности выигрыша первой партии для В и С равны 0, 1 и 0, 2 соответственно; вероятность выиграть во второй партии для В равна 0, 3, для С равна 0, 4. Определить вероятность того, что: а) первым выиграет В; б) первым выиграет С.
18. Из урны, содержащей п шаров с номерами от 1 до n, последовательно извлекаются два шара, причем первый возвращается, если его номер не равен единице. Определить вероятность того, что шар с номером 2 будет извлечен при втором извлечении.
19. Игрок А поочередно играет с игроками В и С, имея вероятность выигрыша в каждой партии 0, 25, и прекращает игру после первого выигрыша или после двух партий, проигранных с любому из игроков. Определить вероятности выигрыша В и С.
20. Двое поочередно бросают монету. Выигрывает тот, у. которого раньше появится герб. Определить вероятности выигрыша для каждого из игроков.
21. В урне имеются 8белых и 6черных шаров. Два игрока последовательно достают по одному шару, возвращая каждый раз извлеченный шар. Игра продолжается до тех пор, покакто-нибудь из них не достанет белый шар. Определить вероятность того, что первым вытащит белый шар игрок, начинающий игру.
22. Послан курьер за документами в 4 архива. Вероятность наличия нужных документа в I-oм архиве – 0, 9; во II-ом – 0, 95; в III-ем – 0, 8; в IV – ом – 0, 6. Найти вероятность Р отсутствия документа только в одном архиве.
23. Найти вероятность того, что откажут два из трех независимо работающих элементов вычислительного устройства, если вероятность отказа первого, второго и третьего элементов соответственно равны 0, 3, 0, 5, 0, 4.
24. В клетке 8 белых и 4 серые мыши. Для лабораторного исследования случайно отбирают трех мышей, не возвращая обратно. Найти вероятность того, что все три мыши белые.
25. В клетке 8 морских свинок. Три из них страдают нарушением обмена минеральных солей. Последовательно без возвращения достают трех животных. Какова вероятность, что они здоровы?
26. В пруду содержатся 12 карасей, 18 лещей и 10 карпов. Выловили три рыбы. Найти вероятность того, что выловили последовательно двух карпов и карася.
27. В стаде 12 коров, из них 4 – симментальской породы, остальные – галштино-фризтской породы. Для селекционной работы отобрали трех животных. Найти вероятность того, что среди них все три симментальской породы.
28. На ипподроме содержатся 10 гнедых лошадей, 3 – серых в яблоко и 7 белых. Для забега случайным образом отобраны 2 лошади. Какова вероятность того, что среди них нет белой лошади?
29. В питомнике содержатся 9 собак, из них 3 колли, 2 боксера, остальные – доги. Случайным образом отбирают трех собак. Какова вероятность того, что среди них хотя бы один боксер?
30. Средний приплод животных равен 4. Появление особей женского и мужского пола равновероятно. Найти вероятность того, что в приплоде две особи мужского пола.
31. В пакете находятся семена, всхожесть которых равна 0, 85. Вероятность того, что растение зацветет, равна 0, 9. Какова вероятность того, что растение, выросшее из наугад взятого семени, зацветет?
32. В пакете находятся семена бобов, всхожесть которых равна 0, 9. Вероятность того, что цветы бобов будут красного цвета, равна 0, 3. Какова вероятность того, что растение из выбранного наугад семени будет иметь красные цветы?
33. Вероятность того, что случайно выбранный человек в течение следующего месяца попадет в больницу, равна 0, 01. Какова вероятность того, что из трех случайно выбранных на улице людей в течение следующего месяца в точности один будет положен в больницу?
34. Доярка обслуживает 4 коровы. Вероятность заболеть маститом в течение месяца для первой коровы равна 0, 1, для второй – 0, 2, для третьей – 0, 2, для четвертой 0, 15. Найти вероятность того, что в течение месяца хотя бы одна корова заболеет маститом.
35. Четыре охотника договорились стрелять по дичи по очереди. Следующий охотник производит выстрел лишь в случае промаха предыдущего. Вероятности попадания в цель каждым из охотников одинаковы и равны 0, 8. Найти вероятность того, что будет произведено три выстрела.
36. Студент изучает химию, математику и биологию. Он оценивает, что вероятности получить «отлично» по этим курсам равны соответственно 0, 5, 0, 3 и 0, 4. В предположении, что оценки по этим курсам независимы, найти вероятность того, что он не получит ни одной оценки «отлично».
37. Студент знает 20 из 25 вопросов программы. Какова вероятность того, что он знает все три вопроса программы, предложенные ему экзаменатором?
38. Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Вероятности попадания в цель первым и вторым охотником равны соответственно 0, 7 и 0, 8. Какова вероятность попадания в волка хотя бы при одном выстреле?
39. Вероятность попадания в мишень при трех выстрелах хотя бы один раз для некоторого стрелка равна 0, 875. Найти вероятность попадания при одном выстреле.
40. Из стада отбирают высокопродуктивных коров. Вероятность того, что случайно отобранное животное окажется высокопродуктивным, равна 0, 2. Найти вероятность того, что из трех отобранных коров только две будут высокопродуктивными.
41. В первой клетке 3 белых и 4 серых кролика, во второй клетке 7 белых и 5 черных кроликов. Из каждой клетки наудачу взяли по одному кролику. Какова вероятность того, что оба кролика белые?
42. Изучалась эффективность двух вакцин на группе животных. Обе вакцины могут вызвать аллергию у животных с равными вероятностями 0, 2. Найти вероятность того, что вакцины не вызовут аллергию.
43. В семье трое детей. Принимая события, состоящие в рождении мальчика и девочки равновероятными, найти вероятность того, что в семье все дети одного пола.
44. Вероятность установления в данной местности устойчивого снежного покрова с октября равна 0, 1. Определить вероятность того, что в ближайшие три года в этой местности устойчивый снежный покров с октября установится, по крайней мере, один раз.
45. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4% всей продукции являются браком, а 75% небракованных изделий удовлетворяют требованиям первого сорта.
46. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0, 7 и 0, 8, производят по одному выстрелу. Определить вероятность хотя бы одного попадания в мишень.
47. Вероятность наступления события в каждом опыте одинакова и равна 0, 2. Опыты производятся последовательно до наступления события. Определить вероятность того, что придется производить четвертый опыт.
48. Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0, 7. При изготовлении такой же детали на втором станке эта вероятность равна 0, 8. На первом станке изготовлены две детали, на втором три. Найти вероятность того, что все детали первосортные.
49. Разрыв электрической цепи может произойти при выходе из строя элемента 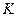 или двух элементов
или двух элементов 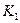 и
и 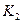 , которые выходят из строя независимо друг от друга соответственно с вероятностями 0, 3; 0, 2 и 0, 2. Определить вероятность разрыва электрической цепи.
, которые выходят из строя независимо друг от друга соответственно с вероятностями 0, 3; 0, 2 и 0, 2. Определить вероятность разрыва электрической цепи.
50. Работа прибора прекратилась вследствие выхода из строя одной лампы из 10-ти. Отыскание этой лампы производится путем поочередной замены каждой лампы новой. Определить вероятность того, что придется проверить 7 ламп, если вероятность выхода из строя каждой лампы равна 0, 1.
51. Вероятность того, что в электрической цепи напряжение превысит номинальное значение, равна 0, 3. При повышенном напряжении вероятность аварии прибора - потребителя электрического тока равна 0, 8. Определить вероятность аварии прибора вследствие повышения напряжения.
52. Вероятность попадания в первую мишень для данного стрелка равна 2/3. Если при первом выстреле зафиксировано попадание, то стрелок получает право на выстрел по другой мишени. Вероятность поражения обеих мишеней при двух выстрелах равна 0, 5. Определить вероятность поражения второй мишени.
53. С помощью шести карточек, на которых написано по одной букве, составлено слово «карета». Карточки перемешиваются, а затем наугад извлекаются по одной. Какова вероятность, что в порядке поступления букв образуется слово «ракета»?
54. Абонент забыл последнюю цифру номера телефона и потому набирает ее наудачу. Определить вероятность того, что ему придется звонить не более чем в три места.
55. Каждое из четырех несовместных событий может произойти соответственно с вероятностями 0, 012; 0, 010; 0, 006 и 0, 002. Определить вероятность того, что в результате опыта произойдет хотя бы одно из этих событий.
56. Какова вероятность извлечь из колоды в 52 карты фигуру любой масти или карту пиковой масти (фигурой называется валет, дама или король)?
57. В ящике имеются 10 монет по 20 коп., 5 монет по 15 коп. и 2 монеты по 10 коп. Наугад берутся 6 монет. Какова вероятность, что в сумме они составят не более одного рубля?
58. В двух урнах находятся шары: в первой 5 белых, 11 черных и 8 красных, а во второй соответственно 10, 8 и 6. Из обеих урн наудачу извлекается по одному шару. Какова вероятность того, что оба шара одного цвета?
59. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна 0, 4. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки.