
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Операції над множинами
|
|
Об’єднання і перетин множин
Розглянуті нижче операції над множинами мають велике значення для розв’язання багатьох задач дискретної математики, особливо тих, що пов’язанні із синтезом дискретних автоматів.
Означення. Об’єднанням множин А і В називається множина, що складається з усіх тих і лише тих елементів, які належать хоча б одній з множин А або В. Позначається  ={x|x
={x|x 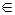 A або х
A або х 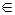 В} (називається сумою або об’єднанням).
В} (називається сумою або об’єднанням).
Таким чином, за наведеним означенням 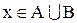 тоді і лише тоді, коли х є елементом хоча б однієї з множин А або В. Наприклад, {1, 2, 3}
тоді і лише тоді, коли х є елементом хоча б однієї з множин А або В. Наприклад, {1, 2, 3} 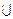 {1, 3, 4}={1, 2, 3, 4}.
{1, 3, 4}={1, 2, 3, 4}.
Об’єднання множини А з порожньою множиною буде давати ту ж саму множину А: 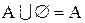 .
.
Аналогічно визначається об’єднання довільної (у тому числі й нескінченної) системи множин. Якщо система містить невелику кількість множин, то їх об’єднання описується явно, наприклад: 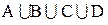 .
.
У випадку, якщо всі множини пронумеровані індексами й належать до системи множин 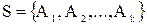 , то їх відображають у вигляді
, то їх відображають у вигляді 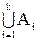 , або
, або 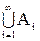 , де S – нескінченна система, і її множини пронумеровані підряд натуральними числами.
, де S – нескінченна система, і її множини пронумеровані підряд натуральними числами.
Для об’єднання множин справедливі комутативний і асоціативний закони:
1. Комутативний закон
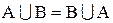 . (1.2)
. (1.2)
2. Асоціативний закон
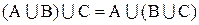 . (1.3)
. (1.3)
Справедливість цих законів випливає з того, що ліва і права частини наведених рівностей складаються з одних і тих самих елементів, а порядок їх об’єднання для множин не має значення.
Означення. Перетином (добутком, перерізом) множин А і В називається множина, що складається з усіх тих і тільки тих елементів, які належать як до множини А, так і до множини В. Позначається 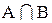 . До цієї множини належать лише спільні елементи множин А і В.
. До цієї множини належать лише спільні елементи множин А і В.
Формальне означення:
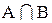 ={x|x
={x|x 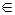 A і х
A і х 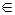 В}. (1.4)
В}. (1.4)
Наприклад, {1, 2, 3} 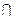 {1, 3, 4}={1, 3}.
{1, 3, 4}={1, 3}.
Для перетину і об’єднання множин властиві такі включення:
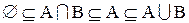 , (1.5)
, (1.5)
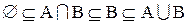 . (1.6)
. (1.6)
Вважається, що дві множини А і В не перетинаються, якщо 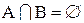 , і перетинаються, якщо
, і перетинаються, якщо 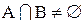 .
.
Перетин множин має комутативну
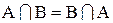 (1.7)
(1.7)
і асоціативну властивість
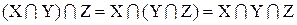 . (1.8)
. (1.8)
Для порожньої множини має місце також співвідношення 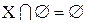 , яке твердить, що перетин будь-якої множини з порожньою множиною дає ту саму порожню множину.
, яке твердить, що перетин будь-якої множини з порожньою множиною дає ту саму порожню множину.
Декартів добуток
Означення. Декартів добуток (прямий добуток) двох множин А і В — це множина усіх можливих впорядкованих пар, у яких перша компонента належить множині А, а друга — множині В.
Декартів добуток двох множин А і В позначається як 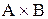 :
:
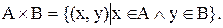 (1.9)
(1.9)
Наприклад, якщо множина А складається з 13 елементів { A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2 }, а множина В – з 4 елементів {червоний, чорний, блакитний, зелений}, то декартів добуток цих множин є 52-елементною множиною (оскільки 13× 4=52) {(A, червоний), (K, червоний),..., (2, червоний), (A, чорний),..., (3, зелений), (2, зелений)}.
Різниця множин
Означення. Різницею множин А і В або відносним доповненням множини В до А називається множина, що складається з усіх тих і лише тих елементів, які належать А і не належать до В. Визначається лише для двох множин.
Наприклад, різниця між натуральними і парними числами являє собою множину всіх непарних натуральних чисел.
Різниця множин А і В позначається як A\B (A/B), або А-В, що відповідає умові {х|х 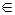 A і х
A і х 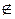 В}, яка визначає ті елементи множини А, що не є елементами множини В. Саму операцію знаходження різниці двох множин називають відніманням множин.
В}, яка визначає ті елементи множини А, що не є елементами множини В. Саму операцію знаходження різниці двох множин називають відніманням множин.
Нехай А ={1, 3, 4, 5}, а B ={1, 2, 3}. Тоді отримана при відніманні множини В від А різниця А–В={4, 5}.
Множина 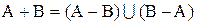 називається симетричною різницею.
називається симетричною різницею.
Якщо А ={1, 3, 4, 5}, а В ={1, 2, 3}, то симетрична різниця А+В={2, 4, 5}.
Теорема. 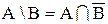 .
.