
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгебра множин
|
|
Алгебра множин створюється з допомогою операцій між підмножинами універсальної множини як сукупність рівностей – тотожностей. Наприклад, для будь-яких підмножин (множин) А, В та С універсальної множини U дійсними є рівності:
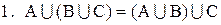 ;
;
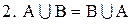 ;
;
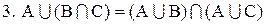 ;
;
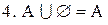 ;
;
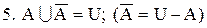 .
.
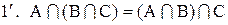 ;
;
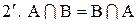 ;
;
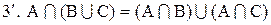 ;
;
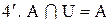 ;
;
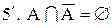 .
.
Кожну з наведених рівностей можна довести, показавши, що будь-який елемент множини, що стоїть з одного боку від знака рівності, належить до множини, яка стоїть з іншого боку від цього знака рівності.
Доведення рівності 3. Доведення складається з двох частин:
1. Нехай 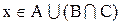 . Тоді
. Тоді 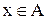 або
або 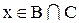 . Якщо
. Якщо 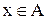 , то
, то 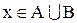 і
і 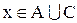 , і таким чином, х є елементом перетину цих множин:
, і таким чином, х є елементом перетину цих множин: 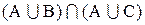 . Якщо
. Якщо 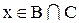 ,
, 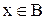 і
і 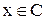 . Отже,
. Отже, 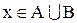 і
і 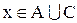 . У цьому випадку х також є елементом перетину
. У цьому випадку х також є елементом перетину 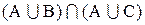 .
.
2. Розглянемо вираз
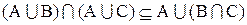 .
.
Нехай 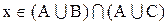 . Тоді
. Тоді 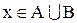 і
і 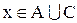 . Отже, або
. Отже, або 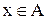 , або
, або 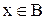 і
і 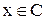 . З цього випливає, що
. З цього випливає, що 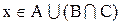 .
.
Тобто х належить як до першої частини рівності 3, так і до другої, що й доводить її.
Рівності 1 та 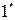 називаються асоціативними законами для об'єднання і перетину, а рівності 2 та
називаються асоціативними законами для об'єднання і перетину, а рівності 2 та 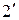 - комутативними законами для цих операцій. Рівності 3 та
- комутативними законами для цих операцій. Рівності 3 та 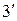 - це дистрибутивні закони для цих операцій.
- це дистрибутивні закони для цих операцій.
Для довільних підмножин А і В універсальної множини U, крім вищезазначених рівностей, справедливі також рівності:
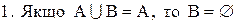 .
.
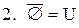 .
.
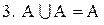 .
.
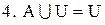 .
.
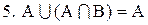 .
.
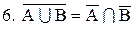 .
.
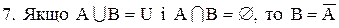 .
.
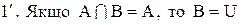 .
.
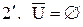 .
.
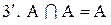 .
.
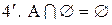 .
.
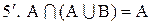 .
.
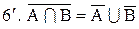 .
.
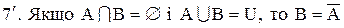 .
.
Деякі з рівностей відомі під спеціальними назвами. Так 3 і 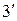 - це закони ідемпотентості; 5 та
- це закони ідемпотентості; 5 та 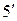 - закони поглинання; 6 та
- закони поглинання; 6 та 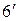 - закони де Моргана.
- закони де Моргана.
Приклад 1. 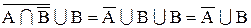 .
.
Приклад 2.
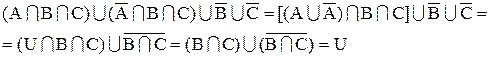
Приклад 3. Довести, що 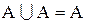 :
:
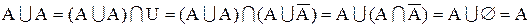 .
.