Властивості бінарних відношень

Кожне бінарне відношення може володіти одним або кількома з існуючих властивостей. Ці властивості визначають вид матриці та графа відношення.

Рефлексивність. Відношення R на множині Х називається рефлексивним, якщо для будь-якого має місце 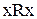, тобто кожен елемент знаходиться у відношенні R до самого себе.

Властивість рефлексивності при заданні відношення матрицею характеризується тим, що всі діагональні елементи матриці дорівнюють 1, а при заданні відношення графом кожен елемент має петлю-дугу (х, х).

Антирефлексивність. Відношення R на множині Х називається антирефлексивним, якщо з 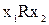випливає, що .

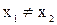Властивість антирефлексивності при заданні відношення матрицею характеризується тим, що всі діагональні елементи є нульовими. При заданні такого відношення графом жодна вершина не має петлі, тобто немає дуг виду (х, х).

Симетричність. Відношення R на множині Х називається симетричним, якщо для пари 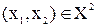з 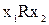слідує 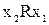(інакше кажучи, для будь-якої пари відношення R виконується або в обидві сторони, або не виконується взагалі).

Матриця симетричного відношення є симетричною відносно головної діагоналі, а в заданому графі для кожної дуги з 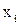в існує протилежний напрямок дуги з в .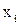

Асиметричність. Відношення R називається асиметричним, якщо для пари 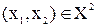з 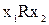випливає, що не виконується 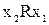(інакше кажучи, що для будь-якої пари відношення R виконується або в один бік, або не виконується взагалі).

Антисиметричність. Відношення R називається антисиметричним, якщо з 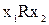та 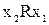, випливає, що .

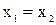Приклад антисиметричного відношення – відношення «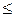» на множині дійсних чисел: якщо 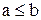та , то .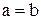

Транзитивність. Відношення R називається транзитивним, якщо з 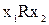та , випливає .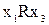

У графа, що задає транзитивне відношення R, для кожної пари дуг, таких, що кінець першої співпадає з початком другої, існує третя дуга, що має загальний початок з першою і загальний кінець з другою.

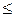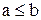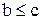Приклад. Відношення «» і «» на множині дійсних чисел транзитивне: якщо і , то .

Антитранзитивність. Відношення R називається антитранзитивним, якщо з 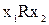і випливає, що не виконується 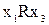.