Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Властивості множин
|
|
Означення. Потужність множини — це узагальнення поняття кількості елементів множини. Потужність множини A позначається як | A | або # A та позначається кардинальним числом.
Потужності множин можна порівнювати. Тобто можливі три випадки:
1. |A|=|B| або A та B рівнопотужні;
2. |A|> |B|або A потужніша від B, тобто A містить власну підмножину, рівнопотужну B, але A и B не рівнопотужні;
3. |A|< |B| або B потужніша від A, в цьому випадку B містить власну підмножину, рівнопотужну А, але А та B не рівнопотужні.
Ситуація, в якій A та B не рівнопотужні, і в жодній з них немає частини, рівнопотужній іншій множині, в теорії множин неможлива.
Означення. Зліченність множини - це така нескінчена множина, елементи якої можна занумерувати натуральним числом. Множина, яка не є зліченною, називається незліченною. Таким чином, будь-яка множина є або скінченою, або зліченною, або незліченною.
Тобто, зліченна множина - це множина, рівнопотужна множині натуральних чисел.
Зліченна множина є найменшою нескінченною множиною в тому розумінні, що в будь-якій нескінченній множини знайдеться зліченна підмножина.
Означення. Скінченна множина – множина, кількість елементів якої скінченна, тобто існує натуральне число, що є числом елементів цієї множини. В інакшому випадку множина є нескінченною.
Функції на множинах (відображення)
Математичне поняття функції виражає інтуїтивне уявлення про те, як одна величина повністю визначає значення іншої величини. Так, значення змінної x однозначно визначає значення виразу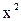 
, а значення місяця однозначно визначає значення наступного за ним місяця. Аналогічно, деякий задуманий наперед алгоритм за варійованими вхідними даними видає певні вихідні значення. Зазвичай розглядають числові функції, які ставлять одні числа у відповідність іншим. Такі функції володіють низкою відмінностей і зручно представляються на рисунках у вигляді графіків.
Існують два визначення функцій.
1) інтуїтивне - поняття функції перекладається звичайною мовою, при цьому використовуючи слова «закон», «правило» або «відповідність».
Означення. Функція f (відображення, операція, оператор) – це закон або правило, згідно якому кожному елементу x з множини Xставиться у відповідність єдиний елемент у з множини Y.
При цьому говорять, що функція f заданана множині X, або що f відображує X в Y.
Якщо елементу 
відповідає елемент 
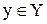, то говорять, що елемент у знаходиться у функціональній залежності f від елементу x. При цьому змінна x називається аргументом функції f або незалежною змінною.
Множина X називається областю задання або областю визначення функції, а елемент у, відповідний конкретному елементу x, – значенням функції f в точці x.
Множина Y всіх можливих значень функції f називається її областю значень або областю зміни.
2) теоретико-множинне - визначення на основі поняття бінарного відношення, яке є більш суворішим.
У теоретично-множинному визначенні функцію f зручно подати як бінарне відношення (тобто множина впорядкованих пар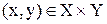 
), яке задовольняє наступній умові: для будь-якого існує єдиний елемент 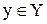такий, що 
.
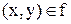Розглянемо дві множини Х та Y.
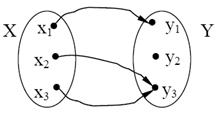
Рисунок 1.7. Відображення множини Х у множину Y
Означення. Якщо кожному елементу відповідає єдиний елемент 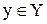, то така відповідність називається відображенням множини Х у множину Y (рис. 1.7).
Позначення: f: X→ Y, f – символ самого відображення.
Означення. Якщо при відображенні f кожний елемент множини Y є образом хоча б одного елементу з множини Х, то f називають сюр’єнктивною функцією або сюр’єнцією (рис. 1.8).
Рисунок 1.8. Ілюстрація відображення сюр’єнції
Приклад. Нехай Х – множина студентів, Y – множина книг. Відображення «студенту х належить книга у» задає сюр’єнцію, оскільки будь-яка книга може належати одному або декільком студентам, а деякі студенти книг взагалі не мають.
Означення. Якщо при відображенні f всі різні елементи множини Х переходять в різні елементи множини Y, то відображення f називають ін’єнктивною функцією або ін’єнцією (рис. 1.9).
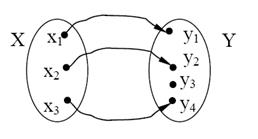
Рисунок 1.9. Ілюстрація відображення ін’єнції
Приклад. Нехай Х – множина студентів, Y – множина стільців в аудиторії. Відображення «студент х сидить на стільці у» задає ін’єнцію, оскільки кожний студент сидить на стільці, але в аудиторії є ще й вільні стільці.
Означення. Якщо при відображенні f кожному елементу відповідає один елемент 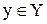, при чому кожному елементу 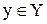відповідає єдиний елемент , то відображення f називається взаємно однозначною функцією (рис. 1.10).
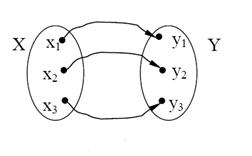
Рисунок 1.10. Ілюстрація взаємно однозначного відображення
Приклад. Нехай Х – множина студентів, Y – множина залікових книжок. Відображення «студенту х належить залікова книжка у» є взаємно однозначним, оскільки певному студенту належить відповідно одна його залікова книжка і навпаки.