На дом.№ 4118, 4122, 4125.

Решение 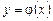дифференциального уравнения

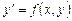(4.1)

называется особым, если в каждой его точке нарушается свойство единственности, т.е. если через каждую его точку 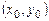, кроме этого решения, проходит и другое решение, имеющее в точке 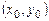ту же касательную, но не совпадающее с решением 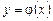в сколь угодно малой окрестности точки 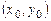. График особого решения будем называть особой интегральной кривой.

Если две кривые 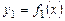и 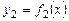имеют общую точку и в этой точке общую касательную, то говорят, что кривые касаются в этой точке.

Условия касания кривыx в т. :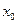

.

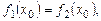
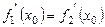Кривая, которая касается каждой кривой семейства

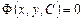
в одной или нескольких точках и притом вся состоит из точек касания, называется огибающей данного семейства.

Теорема. Пусть 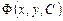– семейство кривых, причем

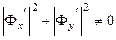в точке .

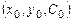Тогда в некоторой окрестности точки 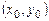точки, лежащие на огибающей 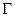этого семейства кривых, удовлетворяют системе:

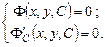(4.2)

Замечание. Теорема утверждает, что если 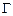– огибающая, то всякая её точка удовлетворяет (4.2). Обратное неверно, т.е. определяемая (4.2) кривая может и не быть огибающей. (Теорема даёт лишь необходимое условие огибающей.) Из решений системы (4.2) огибающие отбираются непосредственной проверкой условий касания.

Если из уравнений системы (4.2) удается исключить параметр C, то уравнение огибающей получается в явном виде, как .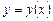

Пример 4.1. 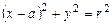. Это уравнение описывает семейство окружностей радиуса 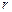, центры которых лежат на оси OX, а параметр 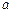есть смещение центров относительно начала координат.

Продифференцировав уравнение по параметру 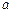, получим 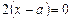. Подставив в уравнение 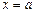и исключив тем самым параметр 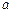, получим 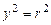, или иначе 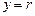и 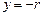- уравнения двух огибающих семейства кривых.

Красивый наглядный пример особого решения дает уравнение Клеро, имеющее вид

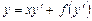. (4.3)

При интегрировании его применим метод введения параметра. Приняв y'=p и подставив в (4.3), получим

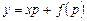. (4.4)

Далее, продифференцировав уравнение (4.4) по переменной 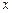, получим

,

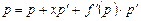откуда

.

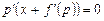Здесь либо 1) 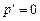, либо 2) .

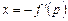Из 1) следует 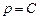. Подставив это в уравнение (4.4), получим 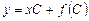- уравнение семейства прямых с угловым коэффициентом 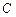, пересекающих ось OY в точках 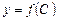. Используя 2), решение можно представить в параметрическом виде:

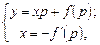(4.5)

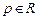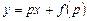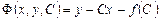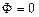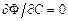где . Нетрудно увидеть, что интегральная кривая, определяемая (4.5), является огибающей семейства прямых . Действительно, в этом случае и огибающая определяется уравнениями и , или

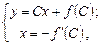(4.5')

где 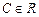, что отличается от (4.5) лишь обозначениями. Если удается исключить С из (4.5'), то особое решение можно получить в явном виде.

4119. Решить уравнение

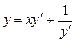. (4.6)

Решение. Подставим 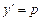, получим

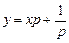. (4.6')

Продифференцировав по 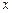, имеем

,

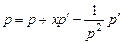откуда

; ; ; .

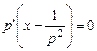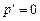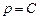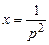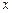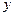
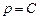Подставив в выражения для и , получим систему уравнений:

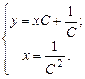(4.7)

Подставив 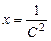в первое уравнение, найдем

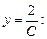
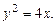(4.8)

Это уравнение параболы, симметричной относительно оси OX. Семейство прямых, описываемых первым уравнением системы (4.7), есть семейство касательных к этой параболе. Таким образом, парабола (4.8) может рассматриваться как огибающая семейства собственных касательных. Такое геометрическое истолкование характерно для уравнения Клеро.