
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
На дом № 2728, 2730, 2732, 2734, 2740, 2743, 2750, 2752.
|
|
Определение. Выражение
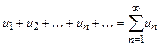 , (9.1)
, (9.1)
в котором 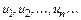 являются членами числовой последовательности
являются членами числовой последовательности 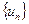 , называется числовым рядом;
, называется числовым рядом; 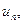 номер которого не фиксирован, называется общим членом ряда.
номер которого не фиксирован, называется общим членом ряда.
Поскольку ряд содержит бесконечное множество слагаемых, их последовательным сложением найти сумму ряда невозможно. Поэтому требуется определить, что считать суммой ряда. Выражения
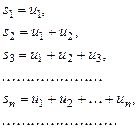
называют частичными суммами ряда (9.1). Эти суммы образуют числовую последовательность
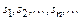 , причём
, причём 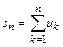 (9.2)
(9.2)
Если существует предел последовательности частичных сумм (9.2), 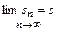 , то ряд (9.1) называется сходящимся, а величина
, то ряд (9.1) называется сходящимся, а величина 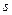 называется суммой ряда
называется суммой ряда 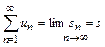 . Ряд называется расходящимся, если последовательность частичных сумм ряда расходится.
. Ряд называется расходящимся, если последовательность частичных сумм ряда расходится.  Ряд
Ряд 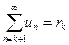 , членами которого являются члены ряда (9.1), начиная с
, членами которого являются члены ряда (9.1), начиная с 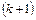 -го, взятые в том же прядке, называется остатком ряда
-го, взятые в том же прядке, называется остатком ряда 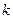 -го порядка.
-го порядка.
Если ряд расходится, то и его остаток любого порядка расходится. Если ряд сходится, то и его остаток 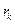 сходится при любом
сходится при любом 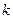 . В этом случае остаток записывается в виде
. В этом случае остаток записывается в виде 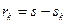 и
и 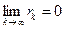 .
.
Пример 9.1. Для числового ряда
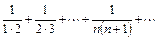 (9.3)
(9.3)
установить сходимость и найти его сумму.
Решение. Преобразуем выражение общего члена ряда:
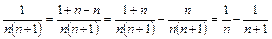 .
.
Частичные суммы ряда 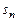 также будут преобразованы:
также будут преобразованы:
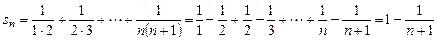 Отсюда следует, что
Отсюда следует, что
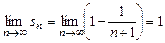 ,
,
т.е. ряд (9.3) сходится и сумма его равна единице.
Пример 9.2. Исследовать на сходимость числовой ряд
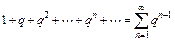
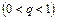 (9.4)
(9.4)
Решение. Этот ряд называется геометрическим, т.к. его члены являются членами геометрической прогрессии со знаменателем 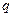 . Запишем частичную сумму ряда
. Запишем частичную сумму ряда
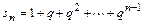 .
.
Вычтем из записанной строки ту же строку, умноженную на 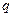 :
:
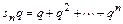 .
.
Получим
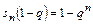 ;
; 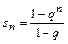 ;
;
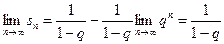 .
.
Последнее имеет место при условии 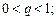 если же
если же 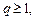 то ряд расходится.
то ряд расходится.
Пример 9.3. Рассмотрим ряд 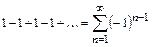 .
.
Решение. Поскольку для этого ряда 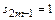 ,
, 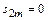 при любом натуральном
при любом натуральном 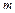 , то последовательность
, то последовательность 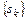 не имеет предела при
не имеет предела при 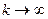 . Следовательно, ряд
. Следовательно, ряд 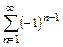 расходится.
расходится.
В приведенных примерах последовательность 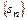 частичных сумм ряда выражалась достаточно просто, так что существование и величина предела
частичных сумм ряда выражалась достаточно просто, так что существование и величина предела 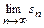 устанавливалась непосредственно. Чаще непосредственный анализ последовательности
устанавливалась непосредственно. Чаще непосредственный анализ последовательности 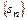 не представляется возможным, поэтому основной задачей в теории числовых рядов является установление сходимости или расходимости ряда без вычисления его суммы.
не представляется возможным, поэтому основной задачей в теории числовых рядов является установление сходимости или расходимости ряда без вычисления его суммы.
Перефразируя критерий Коши сходимости числовых последовательностей, получаем критерий Коши для рядов.
Теорема 9.1 (Критерий Коши).
Числовой ряд 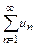 сходится тогда и только тогда, когда для него выполняется условие Коши, состоящее в том, что для любого числа
сходится тогда и только тогда, когда для него выполняется условие Коши, состоящее в том, что для любого числа 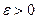 существует номер
существует номер 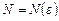 такой, что неравенство
такой, что неравенство
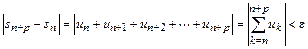
имеет место для любого натурального 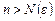 и всех p=1, 2,
и всех p=1, 2, 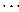 .
.
Приведём формальную запись критерия Коши сходимости ряда:
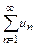 сходится
сходится 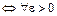
 :
: 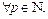
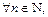
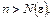
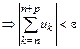 .
.
Замечание. Если условие Коши не выполняется, т.е. 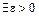
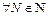
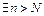
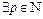

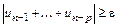 то ряд
то ряд 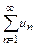 расходится.
расходится.
Следующая теорема является следствием критерия Коши.
Теорема 9.2 (Необходимый признак сходимости ряда).
Если ряд 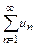 сходится, то
сходится, то
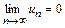 (9.5)
(9.5)
Последнее утверждение получается, если в критерии Коши положить 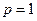 . Заметим, что условие
. Заметим, что условие
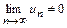 (9.6)
(9.6)
является достаточным условием расходимости ряда. Условие же (9.5), будучи необходимым условием сходимости, достаточным условием сходимости не является. Нужно понимать, что необходимый признак сходимости применяется только для доказательства расходимости числового ряда.
Отметим некоторые свойства сходящихся рядов.
Свойство 1. Отбрасывание любого конечного числа членов ряда не влияет на его сходимость (но не на сумму!).
Свойство 2. Сходимость ряда не нарушится при умножении всех членов ряда на одно и то же число, отличное от нуля.
Свойство 3. Если ряды 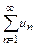 и
и 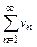 сходятся, то сходится и ряд
сходятся, то сходится и ряд 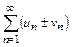 , причём
, причём
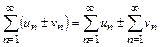 . (9.7)
. (9.7)
О сумме двух расходящихся рядов общего утверждения высказать нельзя. Так, например, сумма двух расходящихся рядов 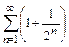 и
и 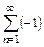 будет сходящимся рядом
будет сходящимся рядом 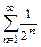 .
.
Заметим, что из сходимости ряда, стоящего в левой части равенства (9.7) не следует сходимость рядов, стоящих в правой части равенства.
Контрольные вопросы.
- Сформулируйте определение числового ряда.
- Дайте определения частичной суммы и остатка числового ряда.
- В каком случае числовой ряд называется расходящимся, а в каком – сходящимся? Чему равна сумма сходящегося ряда?
- Сформулируйте критерий Коши сходимости числового ряда.
- Сформулируйте необходимый признак сходимости числового ряда.
- Перечислите некоторые свойства сходящихся рядов.