На дом № 2754,2756, 2758, 2760, 2765, 2768, 2772, 2774, 2790, 2792.

Заметим, что, поскольку все члены ряда неотрицательны, частичные суммы ряда образуют возрастающую (неубывающую) числовую последовательность 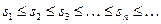. Возможны два случая.

1. Последовательность частичных сумм не ограничена. В этом случае 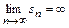и, следовательно, ряд расходится.

2. Последовательность частичных сумм ограничена, т.е. 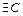такое, что 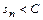при любом значении 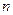. В этом случае, согласно теореме о пределе монотонной ограниченной последовательности, последовательность частичных сумм 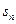и, следовательно, ряд сходятся.

Таким образом, при доказательстве сходимости ряда с неотрицательными членами достаточно установить ограниченность последовательности его частичных сумм.

Рассмотрим также важнейшие признаки сравнения, позволяющие сделать вывод о сходимости либо расходимости ряда, сравнивая его члены с членами другого ряда, поведение которого (сходимость, расходимость) уже известно.

Первый признак сравнения. Пусть даны два ряда с неотрицательными членами:

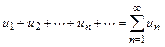(U)

и

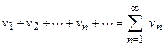(V)

причём

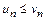
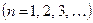. (10.1)

Тогда, если сходится ряд (V), то сходится и ряд (U); если же расходится ряд (U), то расходится и ряд (V).

Этот признак остаётся в силе, если неравенство (10.1) выполняется не для всех n, а лишь начиная с некоторого n=N.

Второй признак сравнения. Если существует конечный и отличный от нуля предел 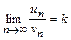, то оба ряда 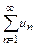и 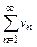вместе сходятся или вместе расходятся.

При исследовании сходимости ряда с помощью теорем сравнения следует выражение общего члена ряда сравнить с общим членом ряда сравнения. Чаще всего в качестве рядов сравнения используют геометрический ряд 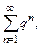гармонический ряд 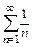и обобщённый гармонический ряд (ряд Дирихле) .

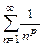Пример 10.1. Исследуем ряд

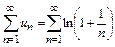. (U)

Решение. Общий член ряда

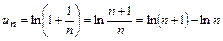. (10.2)

Подставив (10.2) в выражение (9.2) для 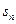, получим:

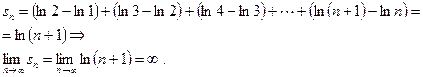
Следовательно, исследуемый ряд расходится.

Пример 10.2. Полученный в примере 10.1 результат используем для доказательства расходимости гармонического ряда

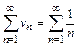. (V)

Решение. Воспользуемся вторым признаком сравнения:

.

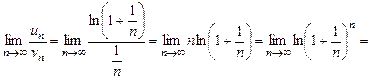
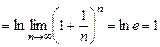Так как предел конечен и отличен от нуля, а ряд (U) расходится, то и ряд (V) (гармонический ряд) тоже расходится.

Пример 10.3. Используем гармонический ряд

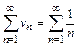(V)

в качестве ряда сравнения при исследовании сходимости ряда

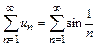. (U)

Найдём предел

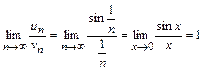
(подстановка 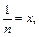при 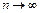получаем 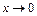). На основании второго признака сравнения, ряд (U) расходится вместе с рядом (V).

Пример 10.4. Исследовать сходимость ряда

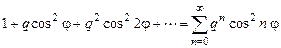
при условии .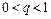

Решение. Сравним этот ряд с геометрическим рядом

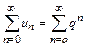. (U)

Поскольку 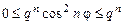, на основании первого признака сравнения можно утверждать, что исследуемый ряд сходится. Можно сказать иначе: исследуемый ряд сходится, т.к. он имеет сходящуюся мажоранту, которой является ряд (U).

Пример 10.5. Исследовать сходимость ряда

.

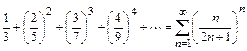Решение. Общий член ряда 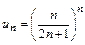. Очевидно, что 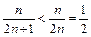. Поэтому 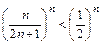. Ряд 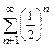– сходящийся геометрический, является мажорантой исследуемого ряда. Отсюда заключаем, что исследуемый ряд сходится.

Пример 10.6. Исследовать сходимость ряда

.

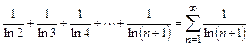Решение. Здесь

, .

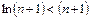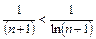Ряд 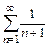– расходящийся гармонический, следовательно, по первому признаку сравнения, исследуемый ряд – расходящийся.

Пример 10.7. Исследовать сходимость ряда

.

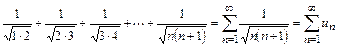Решение. В качестве ряда сравнения выберем гармонический ряд

.

Найдём предел

.

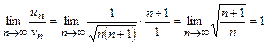Следовательно, по второму признаку сравнения, исследуемый ряд расходится.

Контрольные вопросы.

1. Сформулируйте первый признак сравнения рядов с неотрицательными членами.
2. Сформулируйте второй признак сравнения рядов с неотрицательными членами.
3. Как выглядят геометрический ряд, гармонический ряд, ряд Дирихле?