Занятие 14. Тригонометрические ряды Фурье.

Определение 1. Ряд вида

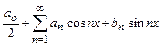(14.1)

называется тригонометрическим рядом. (Здесь знак суммы относится к обоим слагаемым, стоящим справа от него.)

Частичные суммы тригонометрического ряда являются линейными комбинациями функций из системы

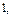
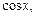
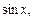
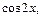
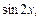
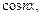
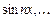(14.2)

Определение 2. Система функций (14.2) называется тригонометрической системой.

Лемма 1. Тригонометрическая система (14.2) имеет следующие свойства.

1. Интеграл на отрезке 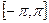от произведения двух различных функций этой системы равен нулю. (Это свойство называется свойством ортогональности системы (14.2)), т.е.

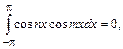
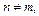
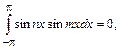
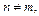(14.3)

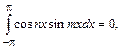
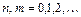
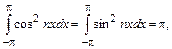
2. 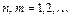(14.4)

Теорема 14.1. Пусть

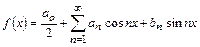(14.5)

и ряд (14.5) сходится равномерно на отрезке 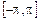, тогда

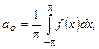
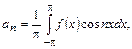
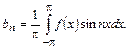(14.6)

Заметим, что формулы (14.6) имеют смысл не только для непрерывных на отрезке 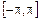функций, а также и для функций, интегралы от которых сходятся абсолютно на этом отрезке. (Говорят, что 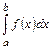сходится абсолютно, если сходится 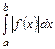.) Этому условию удовлетворяют, в частности, функции, имеющие на отрезке 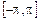конечное число разрывов первого рода и кусочно-дифференцируемые на нём.

Если в точке 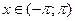существуют конечные пределы 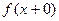, 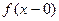и односторонние производные 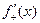и 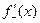, то ряд Фурье функции 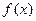сходится в этой точке и его сумма равна

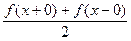. (14.7)

Если существуют конечные пределы 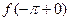, 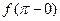и односторонние производные 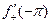и 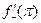, то ряд Фурье функции 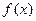сходится в точках 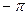и 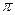и его сумма в этих точках равна

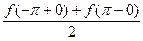. (14.8)

В точках непрерывности функции значения суммы ряда совпадают со значениями функции.

Пример 14.1. Разложить в ряд Фурье функцию

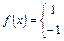
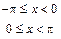
Решение. Вычислим коэффициенты разложения:

,

,

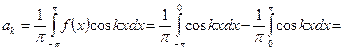
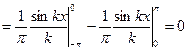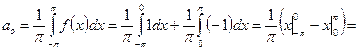
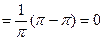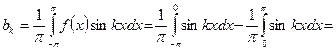
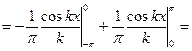
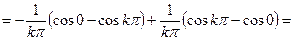
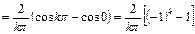
Таким образом, 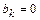при 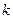чётном 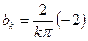и при 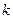нечётном, т.е.

,

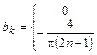
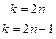следовательно,

.

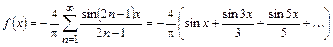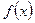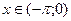Полученный ряд сходится к при и 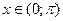, а в точке 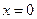, в соответствии с (14.7),

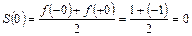. (14.9)

Пример 14.2. Функцию 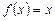, заданную в промежутке 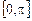, разложить в ряд Фурье по косинусам.

Решение. Продолжив функцию в промежуток 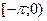чётным образом, получим:

.

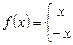
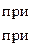
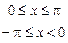В этом случае .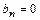

,

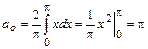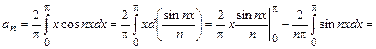
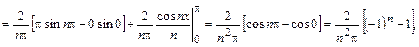
т.е.

,

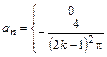
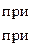
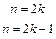следовательно,

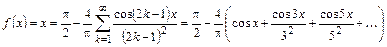
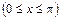
Пример 14.3. Разложить в ряд Фурье в интервале 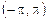функцию

.
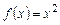