
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. поскольку интеграл по симметричному интервалу берётся от нечётной функции
|
|
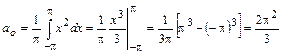 ,
,
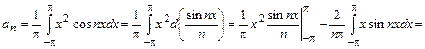
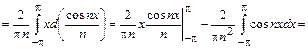
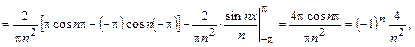

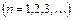
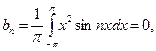
поскольку интеграл по симметричному интервалу берётся от нечётной функции. Ряд Фурье имеет вид
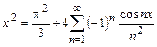 .
.
При 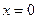 получим полезные соотношения:
получим полезные соотношения:
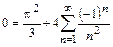 , откуда следует
, откуда следует 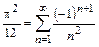 .
.
Пример 14.4. Разложить в ряд Фурье функцию
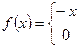
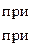
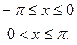
Решение.
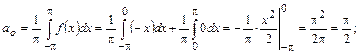
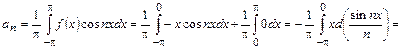
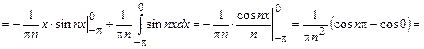
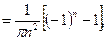 , т.е.
, т.е. 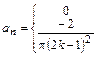
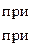
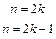 .
.
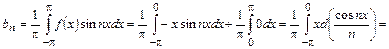
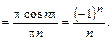
В итоге:
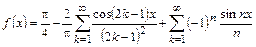 ,
, 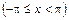
При 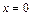 получаем ещё одно полезное соотношение:
получаем ещё одно полезное соотношение:
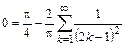 или
или 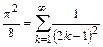 .
.
В случае, если периодическая функция 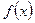 с периодом
с периодом 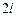 задана в промежутке
задана в промежутке 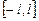 , разложение её в ряд Фурье тоже возможно, однако формулы для вычисления коэффициентов несколько видоизменяются. Если прибегнуть к замене переменной
, разложение её в ряд Фурье тоже возможно, однако формулы для вычисления коэффициентов несколько видоизменяются. Если прибегнуть к замене переменной 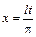 , то получим функцию
, то получим функцию 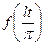 , определённую в промежутке
, определённую в промежутке 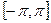 , к которой приложимы все предыдущие соотношения:
, к которой приложимы все предыдущие соотношения:
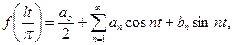
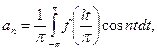
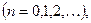
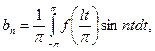
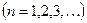
Возвращаясь к прежней переменной 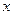 , полагая
, полагая 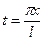 , получим:
, получим:
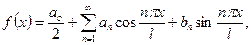 (14.10)
(14.10)
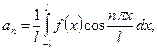
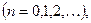 (14.11)
(14.11)
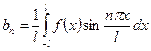 ,
, 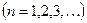 . (14.12)
. (14.12)
Пример 14.5. Разложить в ряд Фурье функцию 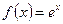 в промежутке
в промежутке 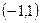 .
.