
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 2. По исходным данным произвести аналитическую группировку с равными интервалами
|
|
По исходным данным произвести аналитическую группировку с равными интервалами. По каждой группе и по совокупности предприятий подсчитать:
1.число предприятий;
2.удельный вес предприятий группы (в % к итогу);
3.размер факторного признака – всего по группе и в среднем на одно предприятие;
4.размер результативного признака - всего по группе и в среднем на одно предприятие;
Результаты представит в статистической таблице. Построить гистограмму и полигон распределения.
| № предприятия | Численность работающих, чел. | Выручка от реализации продукции, млн. руб. |
Используя аналитические группировки, определяют факторные и результативные признаки изучаемых явлений. Факторные признаки – это те признаки, которые оказывают влияние на другие связанные с ними признаки. Результативные признаки изменяются под влиянием факторных.
В нашем случае факторным признаком является численность работающих, а результативным – выручка от реализации продукции.
Проведем аналитическую группировку с равными интервалами. Оптимальное количество групп с равными интервалами приближенно можно определить по формуле американского ученого Стерджеса:
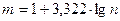 ,
,
где m – количество групп, n – объем совокупности.
В нашем случае
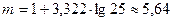 ,
,
значит, в качестве m возьмем 6.
Определим ширину интервала по формуле:
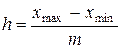
где 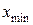 и
и 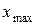 – соответственно наименьшее и наибольшее значение признака в совокупности. В нашем случае
– соответственно наименьшее и наибольшее значение признака в совокупности. В нашем случае
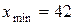 ,
, 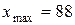 ,
,
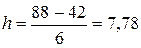 (чел).
(чел).
Значит, в качестве h возьмем 8 человек.
По каждой группе и по совокупности предприятий подсчитаем:
1) число предприятий;
2) удельный вес предприятий группы (в % к итогу);
3) число работающих всего по группе и в среднем на одно предприятие;
4) выручку от реализации продукции всего по группе и в среднем на одно предприятие.
Результаты представим в виде статистической таблицы:
| Число работающих, чел. | Число предприятий | Удельный вес предприятий группы, % | Число работающих в группе, чел. | Число работающих в среднем на одно предприятие, чел. | Выручка в группе, млн.руб. | Выручка в среднем на одно предприятие, млн.руб.а |
| 42-50 | 188, 5 | |||||
| 50-58 | 282, 4 | |||||
| 58-66 | 443, 6 | |||||
| 66-74 | ||||||
| 74-82 | 774, 25 | |||||
| 82-90 |
Из статистической таблицы видно, что
1) на набольшем количестве предприятий работают 66-74 человек (32% предприятий);
2) наибольшую выручку от реализации продукции получают предприятия с наибольшей численностью работающих, наименьшую выручку – предприятия, на которых занято меньше всего человек;
Построим гистограмму и полигон распределения.
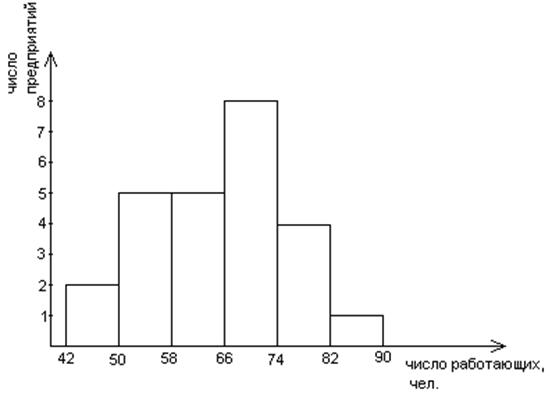
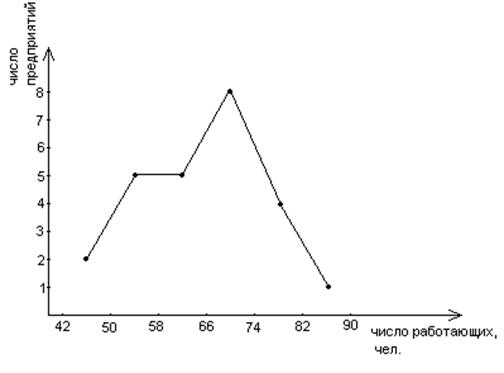
Задача 3. По данным аналитической группировки (задача № 24) по факторному признаку вычислить:
1.среднее значение
- по простой арифметической;
- по арифметической взвешенной;
2.моду и медиану.
Вычисленные значения покажите на графике. Сделайте вывод о распределении предприятий по факторному признаку.
Средняя арифметическая простая вычисляется по формуле:
 .
. 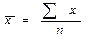
Простая средняя арифметическая численности работающих равна:
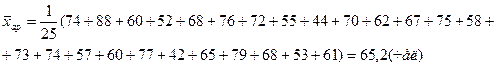
Средняя арифметическая взвешенная из групповых средних определяется по формуле:
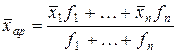 ,
, 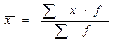
Средняя арифметическая взвешенная численности работающих равна:
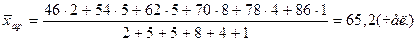 .
.
В данном случае средняя арифметическая простая и средняя арифметическая взвешенная оказались равны. В большинстве же случаев средняя арифметическая простая дает более точный результат. Это связано с тем, что когда отдельные варианты представлены в виде интервалов, в качестве варианта принимают середину интервалов. При этом предполагают, что варианты внутри интервала распределяются равномерно. В действительности распределение вариантов внутри интервала может быть неравномерно и середина интервала может не совпадать со средней величиной в интервале.
Мода – это такое значение варианты, которое чаще всего повторяется в ряду распределения. В интервальном ряду сначала определяется модальный интервал (интервал с наибольшей частотой) и значение моды в середине интервала рассчитывается по формуле:
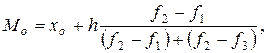
В нашем случае модальным является четвертый интервал, поэтому 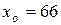 ,
, 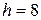 ,
, 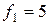 ,
, 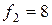 ,
, 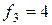 . Таким образом,
. Таким образом,
 (чел.)
(чел.)
Определение моды графическим способом (по гистограмме):
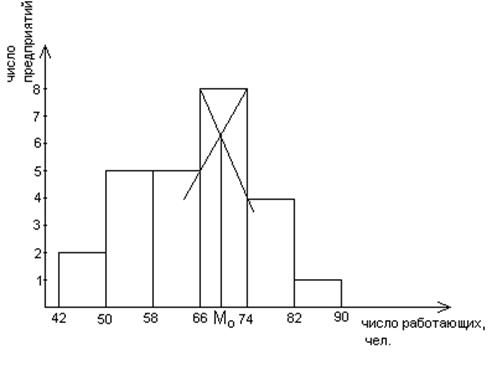
Медианой называют варианту, которая делит ранжированный ряд на 2 равные по объему части. Для интервального ряда медиана вычисляется для середины медианного интервала, за который принимается такой, где сумма накопленных частот превышает половину значений частот ряда распределения:
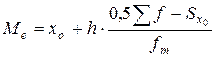
В нашем случае медианным является четвертый интервал. Поэтому 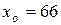 ,
, 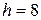 ,
, 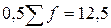 ,
, 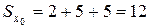 ,
, 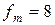 . Таким образом,
. Таким образом,
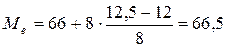
Определение медиана графическим способом (по кумуляте)
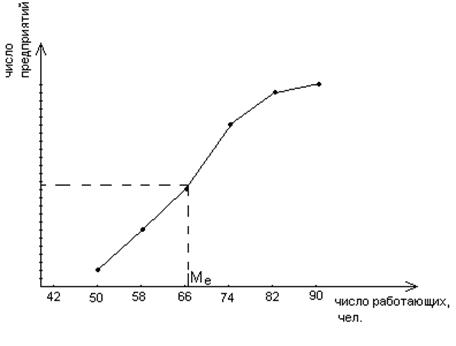
Таким образом, в среднем на каждом предприятии работает 65 человек (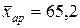 ). Наиболее часто на предприятиях работает по 69 человек (
). Наиболее часто на предприятиях работает по 69 человек (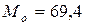 ). ½ всех работающих на предприятиях данной отрасли заняты на предприятиях с численностью до 67 человек, ½ -с численностью 67 человек и более (
). ½ всех работающих на предприятиях данной отрасли заняты на предприятиях с численностью до 67 человек, ½ -с численностью 67 человек и более (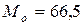 )
)
Тема: «Средние величины и показатели вариации».