
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исходные данные для анализа
|
|
| Средняя выработка одного рабочего, % (х) | Затраты на производство, % (у) |
1. Определение степени однородности совокупностей.
Для выявления степени однородности совокупностей необходимо рассчитать коэффициенты вариаций признаков:
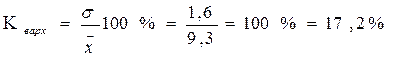
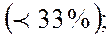
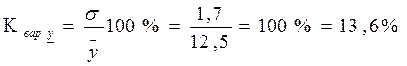
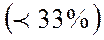 .
.
Вывод: совокупности являются однородными.
2. Определение, являются ли распределения нормальными.
Распределения являются нормальными, если значения средней величины, медианы и моды совпадают или незначительно расходятся.
Медиана 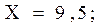
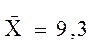 - распределение нормальное.
- распределение нормальное.
Медиана 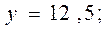
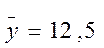 - распределение нормальное.
- распределение нормальное.
3. Составление двух параллельных ранжированных рядов.
| Факторный признак (х) (выработка) | Результативный признак (у) (затраты на производство) |
4. Аналитическая группировка.
Аналитическая группировка производится с целью выявления связи между явлениями.
Порядок выполнения аналитической группировки:
· произвести группировку вариантов факторного признака (х);
· для каждой группы факторного признака выписать соответствующие значения результативного признака (у);
· рассчитать средние значения результативного признака (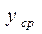 ) каждой группы;
) каждой группы;
· сопоставить изменения результативного признака (у) по мере изменения факторного (х);
· выявить характер связи (прямая, обратная, отсутствует).
Данные для определения характера связи
| Факторный признак (выработка) | Варианты результативного признака (затраты на производство) (у) | Средние значения групп вариант результативного признака (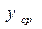 ) )
| |
Варианты (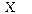 ) )
| Частота (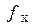 ) )
| ||
| 7, 0 – 8, 7 | 7, 85 | 15; 14 | 14, 5 |
| 8, 7 – 10, 4 | 9, 55 | 12; 13 | 12, 5 |
| 10, 4 – 12, 0 | 11, 25 | 10; 11 | 10, 5 |
Если с ростом значений факторного признака (х) увеличиваются средние групповые значения результативного (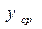 ), то связь прямая, если уменьшаются – обратная.
), то связь прямая, если уменьшаются – обратная.
Аналитическая группировка, выявляя характер связи, не позволяет определить ее форму (линейная, гиперболическая, параболическая).
Вывод: зависимость затрат на производство от выработки обратная.
5. Определение тесноты связи.
Выборочный парный коэффициент корреляции для выборки объемом n, где (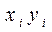 ) – результат i-го наблюдения (i=1, 2, 3, …, n). Определяется по формуле:
) – результат i-го наблюдения (i=1, 2, 3, …, n). Определяется по формуле:
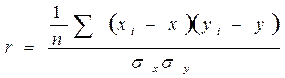 .
.
После преобразований получим упрощенную формулу для расчета r:
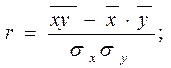
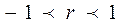 .
.
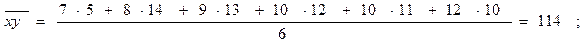
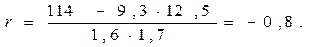
Степень тесноты связи зависит от близости 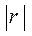 к 1. Связь считается статистически значимой, если
к 1. Связь считается статистически значимой, если 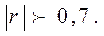 Знак свидетельствует о направлении связи («-» – обратная, «+» - прямая).
Знак свидетельствует о направлении связи («-» – обратная, «+» - прямая).
Вывод: зависимость затрат на производство от выработки обратная, статистически значимая.
6. Построение уравнения регрессии.
После того как с помощью корреляционного анализа выявлено наличие статистической связи между переменными, переходят к математическому описанию зависимости с использованием регрессивного анализа. Результатом такого анализа является уравнение (обычно линейное), выражающее математическую зависимость результативного признака (у) от факторного (х):
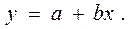
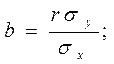
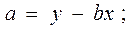
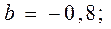
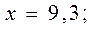
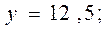

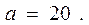
Уравнение регрессии: 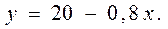
Тема: «Анализ развития социально – экономических явлений. Ряды динамики».
Задача 13. Определите среднесписочную численность работников организации, если за ноябрь списочная численность составляла:
с 1 по 9 – 70 человек
с 10 по 16 – 73 человека
с 17 по 25 – 75 человек
с 26 по 30 – 74 человека
Решение задачи 13:
Используем формулу средней арифметической взвешенной:
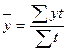 ,
,
где у – уровни, сохраняющиеся неизменными в течение времени t.
Расчеты произведем в таблице:
| Календарные периоды ноября | Число работников (у) | Длина периода, дней (t) | Число человеко-дней (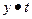 ) )
|
| 1-9 | |||
| 10-16 | |||
| 17-25 | |||
| 26-30 | |||
| Итого | х |

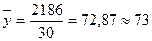 (человека)
(человека)
Таким образом, среднесписочная численность работников организации составляет 73 человека.
Задача 14. Динамика балансовой прибыли предприятий транспорта и связи города характеризуется следующими данными:
| Показатель | Годы | |||
| 1-ый | 2-ой | 3-ий | 4-ый | |
| Темпы прироста к предыдущему году, % |
Определите:
- базисный и среднегодовой темпы роста и прироста за 4 года.
- прогноз базисных темпов роста балансовой прибыли за 5-летний период при условии сохранения среднегодового темпа роста.
Решение задачи 14:
1. Преобразуем темпы прироста в коэффициенты роста:

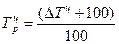
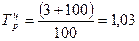
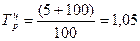
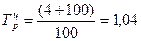
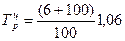
Базисные темп роста и прироста за весь исследуемый период:

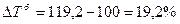
Среднегодовые темпы роста и прироста:
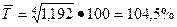
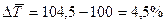
2. 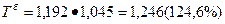
Задача 15. Имеются следующие данные об изменении номинальной среднемесячной заработной платы одного работника и потребительских цен:
| Месяцы | Изменение в % к предыдущему месяцу | |
| номинальной среднемесячной заработной платы одного работника | потребительских цен | |
| Январь | 78, 7 | 108, 4 |
| Февраль | 103, 2 | 104, 1 |
| Март | 114, 8 | 102, 8 |
| Апрель | 103, 0 | 103, 0 |
| Май | 103, 4 | 102, 2 |
| Июнь | 109, 7 | 101, 9 |
Определите:
1) Базисные темпы роста в июне по сравнению с декабрем
2) Коэффициент опережения
3) Индекс реальной заработной платы в июне по сравнению с декабрем.
Сделайте выводы.
Решение задачи 15:
1) 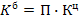
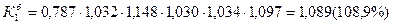
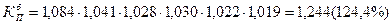
2) 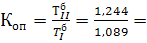

3)  87, 5 – 100 = -12, 5%
87, 5 – 100 = -12, 5%
Следовательно, рост цен опережал рост номинальной заработной платы на 14, 2% в результате чего реальная заработная плата снизилась на 12, 5 %.
Задача 16. Имеются следующие данные о численности населения РФ с денежными доходами ниже величины прожиточного минимума, млн. чел.:
| IV квартал базисного года | Кварталы отчетного года | |||
| I | II | III | IV | |
| 23, 2 | 31, 6 | 29, 8 | 26, 7 | 20, 9 |
Определите:
1. цепные темпы роста и прироста;
2. средний квартальный уровень ряда динамики в отчетном году;
3. средний квартальный темп роста (снижения);
4. ориентировочную численность малоимущего населения в I квартале будущего года.
Сделайте выводы.
Решение задачи 16:
1. 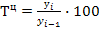 ;
; 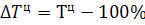
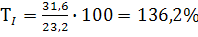 136, 2 - 100 = 36, 2%
136, 2 - 100 = 36, 2%
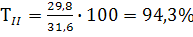 94, 3 - 100 = - 5, 7%
94, 3 - 100 = - 5, 7%
 89, 6 - 100 = - 10, 4%
89, 6 - 100 = - 10, 4%
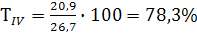 78, 3 – 100 = - 21, 7%
78, 3 – 100 = - 21, 7%
2. 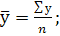
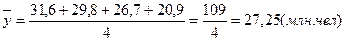
3. 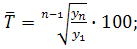
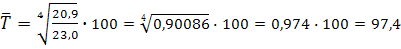 %
%
4. 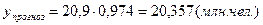
Вывод: При среднеквартальном темпе снижения 97, 4% о риентировочная численность малоимущего населения в 1 квартале будущего года составит 20, 375 млн. человек.
Тема: «Индексный метод в статистическом анализе»
Задача 17. Имеются данные о потреблении овощей и бахчевых в домашних хозяйствах региона (в среднем на члена домохозяйства в месяц, кг.)
| Квартал | Годы | ||
| 1 -й | 2 - й | 3 - й | |
| I | 6, 6 | 6, 3 | 6, 0 |
| II | 5, 9 | 5, 5 | 5, 2 |
| III | 9, 6 | 9, 1 | 8, 6 |
| IV | 7, 7 | 7, 3 | 6, 9 |
Для анализа сезонности потребления овощей и бахчевых и прогноза их среднемесячного потребления по кварталам на предстоящий год исчислите:
1. индексы сезонности потребления методом простой средней;
2. постройте график сезонной волны;
3. осуществите прогноз потребления овощей и бахчевых по кварталам предстоящего года с учетом сезонности, если их годовое потребление в среднем на члена домохозяйства предполагается в объеме 78 кг.
Сделайте выводы.
Решение задачи 17:
1. Для выполнения расчетов составим вспомогательную таблицу:
| Квартал | Годы | 
| 
| 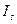
| Прогноз | ||
| 1-й | 2-й | 3-й | |||||
| I | 6, 6 | 6, 3 | 6, 0 | 18, 9 | 6, 3 | 89, 3 | 5, 8 |
| II | 5, 9 | 5, 5 | 5, 2 | 16, 6 | 5, 53 | 78, 4 | 5, 1 |
| III | 9, 6 | 9, 1 | 8, 6 | 27, 3 | 9, 1 | 128, 9 | 8, 4 |
| IV | 7, 7 | 7, 3 | 6, 9 | 21, 9 | 7, 3 | 103, 4 | 6, 7 |
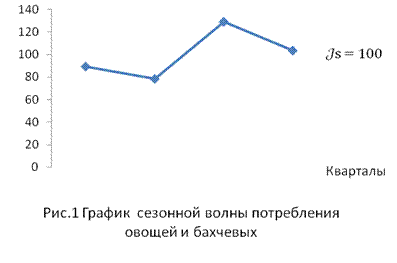
| Итого | 29, 8 | 28, 2 | 26, 7 | 84, 7 | 7, 06 | 6, 5 |
Формулы для расчета:
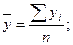
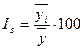
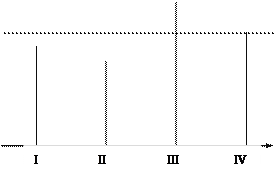
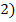
3) Среднемесячное потребление в прогнозируемом году:
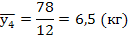
в т.ч. с учетом сезонности в I кв. 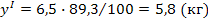
II кв. 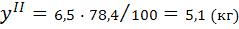
III кв. 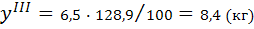
IV кв. 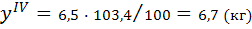
Выводы:
1. Потребление овощей и бахчевых в домохозяйствах имеет сезонный характер.
2. Наибольшее потребление наблюдается в Ш квартале, наименьшее – во втором.
Задача 18. Имеются следующие данные о производстве одноименной продукции и ее себестоимости по двум малым предприятиям:
| Предприятия | Доля предприятий в производстве продукции, % | Себестоимость единицы продукции, руб. | ||
| Базисный период (dо) | Отчетный период (d1) | Базисный период(zo) | Отчетный период(z1) | |
| А | ||||
| В | ||||
| Итого | Х | Х |
Определите:
1) индексы себестоимости продукции по каждому предприятию;
2) для двух предприятий вместе:
- индекс средней себестоимости;
- среднее изменение себестоимости;
- индекс структурных сдвигов.
Сделайте выводы.
Решение задачи 18:
1) 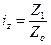 ;
; 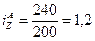 (120%);
(120%);
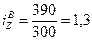 (130%);
(130%);
2) 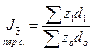 ;
; 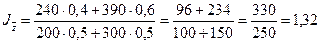 (132%)
(132%)
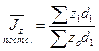 ;
; 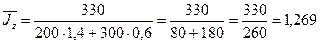 (126, 9%)
(126, 9%)
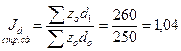 (104%)
(104%)
Выводы:
- себестоимость единицы продукции на малом предприятии А повысилась на 20%, на малом предприятии В – на 30%;
- по двум предприятиям вместе средняя себестоимость выросла на 32%, в т.ч. за счет
повышения себестоимости на каждом предприятии она выросла в среднем на 26, 9%,
а за счет структурных сдвигов - еще на 4%. Структурные сдвиги проявились в том, что в производстве продукции повысилась доля предприятия В с более высоким уровнем себестоимости.
Задача 19. Потребление бытовых услуг населением области характеризуется следующими показателями:
| № п/п | Услуги | Стоимость бытовых услуг в I квартале в текущих ценах, млн.руб. | Изменения объема продаж в сопоставимых ценах в IV квартале к I кварталу, % |
| Прачечных | 2, 6 | -20 | |
| Парикмахерских | 3, 9 |
Определите:
1. общий индекс физического объема предоставляемых услуг;
2. общий индекс цен на бытовые услуги, если известно, что общий объем бытовых услуг в текущих ценах вырос на 15%
3. абсолютное изменение стоимости бытовых услуг по двум видам вместе за счет изменения их физического объема.
Сделайте выводы.
Решение задачи 19:
1. Индивидуальные индексы физического объема продаж по видам услуг:
прачечных 
парикмахерских 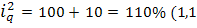 )
)
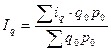 ;
; 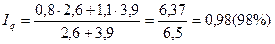
2. 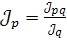
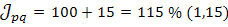
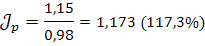
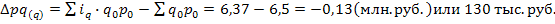
Выводы:
В 1V квартале по сравнению с 1 кварталом количество услуг, предоставляемых прачечными и парикмахерскими, снизилось на 2%, цены на эти бытовые услуги выросли на 17, 3%. Абсолютное снижение стоимости предоставляемых бытовых услуг по двум видам вместе за счет уменьшения их физического объема составило 130 тыс. руб.
Задача 20. Имеются следующие данные об обороте общественного питания по двум городам:
| Город | Оборот общественного питания отчётного периода, млн. руб. | Индексы оборота общественного питания в отчётном периоде по сравнению с базисным, % | |
| в текущих ценах | в сопоставимых ценах | ||
| А | 15, 1 | ||
| В | 12, 4 |
Определите:
1) индексы цен по каждому городу;
2) общий индекс цен по двум городам вместе;
3) абсолютное изменение оборота общественного питания вследствие изменения цен.
Сделайте выводы.
Решение задачи 20:
1) 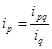 ;
;
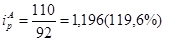
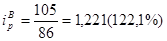
2) 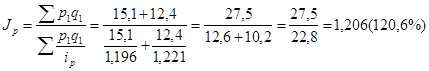
3) 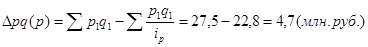
Выводы:
Цены на услуги общественного питания в городе А повысились на 19, 6%, в городе В – на 22, 1%, по двум городам вместе – на 20, 6%; оборот общественного питания вследствие изменения цен увеличился на 4, 7 млн. руб.