Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случайная величина. Числовые характеристики случайных величин
|
|
Понятие случайного события недостаточно для описания результатов наблюдений величин, имеющих числовое выражение. Например, при анализе прибыли предприятия в первую очередь интересуются ее размерами. Поэтому понятие случайного события дополняется понятием случайной величины.
Случайной величиной (СВ) называют величину, которая в результате наблюдения принимает значение, зависящее от случайных обстоятельств.
Объем ВНП, количество реализованной продукции, прибыль фирмы, размер чистого экспорта за год и т. д. являются случайными величинами.
Различают дискретные и непрерывные СВ. Дискретной называют такую СВ, которая принимает отдельные значения с определенными вероятностями. Непрерывной называют такую СВ, которая может принимать любое значение из некоторого конечного или бесконечного промежутка. Например, можно считать, что число покупателей в магазине, побывавших там в течение дня; число автомобилей, ремонтируемых еженедельно в данной мастерской; число находящихся в аэропорту самолетов являются дискретными СВ. Однако большинство СВ, рассматриваемых в экономике, имеют настолько большое число возможных значений, что их удобнее представлять в виде непрерывных СВ. Например, курсы валют, доход, объемы ВНП, ВВП и т. п. обычно рассматриваются как непрерывные СВ.
Законом распределения вероятностей называется функциональная зависимость вероятности 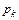 того, что дискретная случайная величина примет значение
того, что дискретная случайная величина примет значение 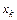 .
.
Любую функцию, а значит и случайную дискретную величину можно задать тремя способами:
- Табличным (таблица);
- Графическим (график, гистограмма); - наглядность
- Аналитическим (уравнение). p = f (x). - описывает характер распределения для любого числа испытаний и любой постоянной вероятности появления события при каждом из них
Функцией распределения СВ X называют функцию 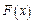 , определяющую вероятность того, что случайная величина X принимает значение меньше, чем заданная величина х, т. е.
, определяющую вероятность того, что случайная величина X принимает значение меньше, чем заданная величина х, т. е.
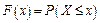
Во многих практических случаях информация о СВ, которую дает закон распределения или функция распределения, является избыточной.
Числа, которые позволяют наиболее простым способом характеризовать распределение, называют первичными описательными статистиками.
Компактное описание группы при помощи первичных статистик позволяет анализировать результаты измерений. Числа, характеризующие данные по уровню выраженности измеренного признака называют мерами центральной тенденции. Существуют три способа определения «центральной тенденции»: мода, медиана и выборочное среднее.
Мода — это такое значение из множества измерений, которое встречается наиболее часто. Моде соответствует вершина графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным. Например, среди значений признака (3, 7, 3, 5, 7, 8, 7, 6) мода Мо = 7 как наиболее часто встречающееся значение. Когда распределение имеет несколько мод, то говорят что оно мультимодально (частный случай - бимодальность). Мультимодальность дает важную информацию о природе исследуемой переменной. Так, например в социологических опросах, если переменная означает отношение к чему-то, то мультимодальность может означать, что существует несколько определенных различных мнений. Когда все значения встречаются одинаково часто, принято считать, что такое распределение не имеет моды.
Медиана — это такое значение признака, которое делит упорядоченное множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая — больше. Таким образом, первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом:
· если данные содержат нечетное число значений (8, 9, 10, 13, 15), то медиана есть центральное значение, т. е. Md= 10;
· если данные содержат четное число значений (5, 8, 9, 11), то медиана есть точка, лежащая посередине между двумя центральными значениями, т. е. Md = 8, 5.
Среднее определяется как сумма всех значений, деленная на их количество. Если х1, х2,..., хi,..., хn наблюдаемые значения, то среднее значение определяется по формуле:
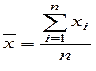
Наиболее очевидной и часто используемой мерой центральной тенденции является среднее значение. Но его использование ограничивается тем, что на величину среднего влияет каждое отдельное значение. (Если какое-нибудь значение в группе увеличится на с, то среднее увеличится на c/n.) Таким образом, среднее значение весьма чувствительно к «выбросам» — экстремально малым или большим значениям переменной.
Пример: если 9 человек имеют месячный доход от 500 до 600 тыс. рублей, со средним 560 тыс. рублей, а доход десятого составляет 10 000 тыс. рублей, то средний доход для этих 10 человек составит 1504 тыс. рублей.
Пример (более подробный): - показать 1 из 2
| Номер набл. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||
| Доход | ||||||||||||||||||||
| Ср= | Мо= | Мд= | ||||||||||||||||||
Цифра среднего значения не позволяет судить обо всей группе, и в качестве меры центральной тенденции следовало бы избрать медиану или моду, которые не чувствительны к «выбросам». Например, если в рассмотренном примере наибольшее значение увеличить или уменьшить на порядок, то ни мода, ни медиана не изменятся.
В официальной статистике США именно медиана используется при оценке доходов населения.
Каждая мера центральной тенденции обладает характеристиками, которые делают ее ценной в определенных условиях. Если распределение унимодальное и симметричное, то эти меры совпадают. Чем больше отклонение от симметричности, тем больше расхождение между значениями этих мер центральной тенденции. Следовательно, по величине расхождения можно судить о том, насколько симметрично или асимметрично распределение.
Для детального анализа поведения СВ нужна числовая оценка разброса возможных значений СВ относительно ее среднего значения.
Наиболее простой и очевидной мерой изменчивости является размах, указывающий на диапазон изменчивости значений.
Размах (Range) – это просто разность максимального и минимального значений: 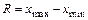
Ясно, что это очень неустойчивая мера изменчивости, на которую влияют любые возможные «выбросы».
Основной характеристикой изменчивости является дисперсия, которая определяется как среднее всех квадратов отклонений от среднего значения: рисунок
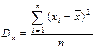 |
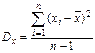 При ограниченном количестве данных большие отклонения от среднего значения, которые могли бы существенно увеличить дисперсию, маловероятны. Поэтому для вычислений, как правило, используется формула выборочной (эмпирической) дисперсии отличающаяся знаменателем:
При ограниченном количестве данных большие отклонения от среднего значения, которые могли бы существенно увеличить дисперсию, маловероятны. Поэтому для вычислений, как правило, используется формула выборочной (эмпирической) дисперсии отличающаяся знаменателем:
.
Свойства дисперсии:
· Если значения не отличаются друг от друга (равны между собой) — дисперсия равна нулю. Это соответствует отсутствию изменчивости в данных.
· Прибавление одного и того же числа к каждому значению переменной не меняет дисперсию:
· Прибавление константы к каждому значению переменной сдвигает график распределения этой переменной на эту константу (меняется среднее), но изменчивость (дисперсия) при этом остается неизменной.
· Умножение каждого значения переменной на константу с изменяет дисперсию в с2 раз:
· При объединении двух групп с одинаковой дисперсией, но с разными средними значениями дисперсия увеличивается. Например, если одна группа содержит значения: 1, 1.1, 1, 1, а другая группа — значения 3, 3, 3, 3, 3, то дисперсии этих групп одинаковы и равны 0. Если же объединить эти две группы, то дисперсия будет равна не 0, а 1.
Дисперсия имеет размерность, равную квадрату размерности СВ. Чтобы представить разброс значений СВ в тех же единицах, что и саму СВ, используется среднее квадратическое отклонение, которое определяется как квадратный корень из дисперсии и традиционно обозначается 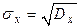 .
.
Чтобы оценить разброс значений СВ в процентах относительно ее среднего значения вводится коэффициент вариации Vx, рассчитываемый по формуле: