Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие о функциональной, статистической и корреляционной связях
|
|
В естественных науках большей частью имеют дело со строгими (функциональными) зависимостями, при которых каждому значению одной переменной соответствует единственное значение другой. Пример: Зная признак-фактор можно найти признак-результат (например, зная валовой сбор и площадь посева зерновых культур, можно абсолютно точно найти их урожайность).
Таких строгих зависимостей в экономике практически нет. Во-первых, ряд факторов нет возможности учесть; во-вторых, многие воздействия носят случайный характер. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная: одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот). Поэтому в экономике говорят не о функциональных, а о корреляционных, либо статистических зависимостях. Нахождение, оценка и анализ таких зависимостей, построение формул зависимостей и оценка их параметров являются одним из важнейших разделов эконометрики.
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. Такую статистическую зависимость называют корреляционной.
Термин корреляция (от английского correlation – согласование, взаимосвязь).
Корреляция – мера согласованности одного признака с другим, с несколькими, либо взаимная согласованность группы признаков.
В корреляционных связях между влиянием факторного и результативного признаков нет полного соответствия, воздействие факторов проявляется лишь при наблюдении за большим количеством фактических данных. Это связано с воздействием на результативный признак большого числа факторных (например, продуктивность скота зависит от породы, уровня кормления, содержания и др.).
Корреляционная связьотражает тот факт, что изменения одного признака находятся в некотором соответствии с изменениями другого признака. (Примеры: расходы на рекламу за предыдущий месяц и объем торговли в текущем месяце, или температура воздуха и объем продажи мороженого).
Но корреляционные методы не выявляют причинно-следственную связь изменений двух признаков, а лишь указывают на наличие некоторого соответствия. Признаки могут находиться не только во взаимной зависимости друг от друга, но и оба в зависимости от какого-либо третьего воздействия, не включенного в область рассмотрения. (Пример: можно заметить строгую прямо пропорциональную зависимость между числом проданных в наблюдаемый период порций мороженого и числом проданных солнцезащитных очков, но не нужно рассматривать эти события как причину и следствие – на обе величины влияет третья – климат).
- Понятие корреляционной модели. Виды КМ
Корреляционно-регрессионный анализ предназначен для изучения корреляционных связей. Он позволяет измерить тесноту связи двух и большего числа признаков между собой и определить аналитическое выражение (уравнение регрессии), описывающее эту связь. Уравнение регрессии и называют «корреляционная модель».
Определение:
КМ - математическое выражение типа уравнения, в котором выражается взаимосвязь между результивным показателем и каким-то (какими-то) факторными показателями.
Можно также дать и другое определение:
КМ –математическое выражение типа уравнения, которое показывает, на сколько единиц изменится результативный показатель при изменении факторного показателя на единицу.
Виды КМ:
· По числу факторов, учтенных в КМ, их можно подразделить на одно- и многофакторные
· По характеру взаимосвязи корреляционные модели могут быть линейными и нелинейными
Примеры:
1) Линейная однофакторная КМ: зависимость объема продаж от цены товара.
В общем виде модель имеет вид
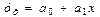 |
где yх – ожидаемое значение результативного показателя, который формируется под воздействием вектора-фактора х.
х – факторный показатель.
а1 – коэффициент регрессии, который показывает, на сколько единиц изменяется результативный показатель при изменении фактора на 1.
а0 – свободный член, который выражает влияние неучтенных факторов.
И свободный член и коэффициент регрессии может иметь как положительное, так и отрицательное значение.
2) Линейная многофакторная КМ: зависимость объема продаж от цены товара и затрат на рекламу.
В общем виде модель имеет вид
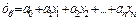 |
3) Нелинейная модель
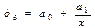 | 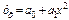 | |||
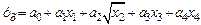 |
Мерой измерения тесноты связи служит коэффициенты:
| линейной корреляции | r |
| корреляционного отношения | η |
| корреляции рангов | rp |
| регрессии | R |
| ассоциации | ra |
| взаимной сопряженности | rc |
| индекса корреляции | Ir |
| множественной корреляции | rм |
Основные этапы построения КМ:
| 1) выбор результативных и факторных показателей | |||||||
| 2) сбор информации и проверка ее на достоверность | |||||||
| 3) выбор вида | |||||||
| 4) расчет параметров и характеристик КМ | |||||||
| 5) анализ использования ресурсов на основе КМ и планирование показателей |
- Линейная корреляция.
Предположим, что мы располагаем выборкой данных о какой-то группе объектов. Пусть эти объекты обладают общими родовыми особенностями (примерно одинаковы). Пусть, к тому же, у каждого из объектов можно количественно измерить, как минимум, два каких-либо параметра. При этих обстоятельствах открывается возможность для подсчета линейной корреляции между двумя (или более) признаками, присущими этим объектам.
Требования и ограничения. Необходимо иметь в виду, что сопоставляемые характеристики должны быть, во-первых, внутренне присущи объектам и, во-вторых, быть количественно-измеряемыми. Ввиду того, что расчет линейной корреляции проводится с использованием средних значений и дисперсий, следует также помнить, что эта процедура требует нормальности распределения признака. Также следует помнить, что никакая корреляция вообще не устанавливает зависимости одного обстоятельства от другого, а лишь является мерой совместной вариации двух величин. И, наконец, линейная корреляция потому и называется линейной, что способна дать ответ о взаимосвязи изменений того и иного свойства объекта только тогда, когда возрастание-убывание значения признака происходит по линейному закону.
Сейчас, для простоты понимания, будем говорить о линейной корреляции между двумя признаками. Связь можно представить графически
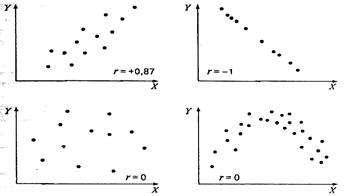
В качестве числовой характеристики вероятностной связи используют коэффициенты корреляции.
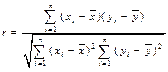 Коэффициент корреляции – это количественная мера силы и направления вероятностной взаимосвязи двух переменных
Коэффициент корреляции – это количественная мера силы и направления вероятностной взаимосвязи двух переменных
Эту формулу можно также записать в виде:
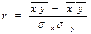 |
Коэффициент корреляции принимает значения в диапазоне от — 1 до +1. Показателем силы связи является абсолютная величина коэффициента корреляции.
| значение r, ± | 0, 16-0, 20 | 0, 21-0, 30 | 0, 31-0, 40 | 0, 41-60 | 0, 61-0, 80 | 0, 81-0, 90 | 0, 91-1 |
| связь | плохая | слабая | умеренная | средняя | высокая | очень высокая | полная |
Направление связи определяется знаком коэффициента корреляции. Если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь называется прямой (положительной); если возрастанию значений одной переменной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной).
- Уравнение регрессии
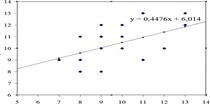
На практике связь между двумя переменными, если она есть, является вероятностной и графически выглядит как облако рассеивания эллипсоидной формы. Этот эллипсоид, однако, можно представить (аппроксимировать) в виде прямой линии, или линии регрессии.
«линия регрессии»–линия наилучшей подгонки под экспериментальные точки
Линия регрессии — это прямая, построенная методом наименьших квадратов: сумма квадратов расстояний (вычисленных по оси y) от каждой точки графика рассеивания до этой прямой является минимальной:
Или
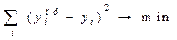
где 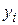 — фактическое i -значение y,
— фактическое i -значение y,
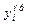 — оценка i -значения y при помощи уравнения регрессии, или предсказанное значение
— оценка i -значения y при помощи уравнения регрессии, или предсказанное значение
Уравнение регрессии имеет вид: 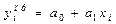 ,
,
где 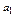 — коэффициент регрессии, задающий угол наклона линии регрессии;
— коэффициент регрессии, задающий угол наклона линии регрессии;
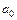 — свободный член, определяющий точку ее пересечения c осью y.
— свободный член, определяющий точку ее пересечения c осью y.
Коэффициент регрессии и свободный член теоретически можно определить с помощью метода наименьших квадратов. Рассмотрим самый простой случай – линейную однофакторную модель.
Известны значения х и 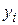 .
. 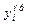 зависит от хi
зависит от хi 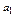 и
и 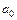 - неизвестные величины
- неизвестные величины
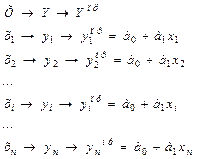
Как уже говорилось 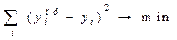
Подставим в это уравнение вместо 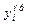 его значение
его значение 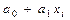 ,
,
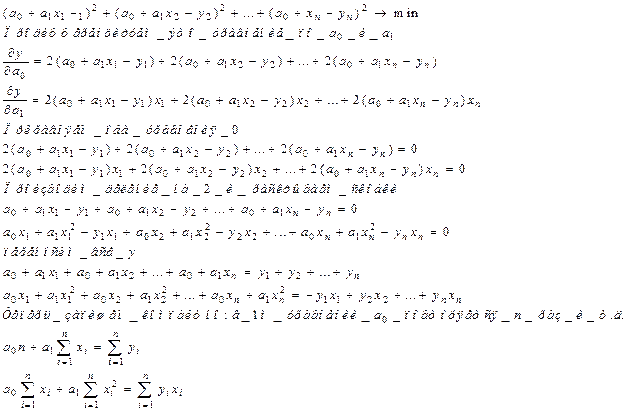
Теперь, произведя несложные вычисления, можем решить систему уравнений и определить 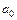 и
и 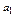
Пример:
| № | Урожайность зерновых, ц с 1 га | Внесение удобрений, ц д.в. на 1 га |
| 38, 2 | ||
| 4, 4 | ||
| … | ||
| 40, 8 |
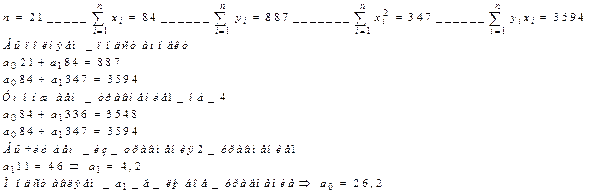
Случай, разобранный сейчас, самый простой. Аналогично выводятся коэффициенты в уравнении множественной линейной регрессии, только вывод будет более громоздким.
Вывод уравнения имеет важное теоретическое значение, но этот процесс, естественно, можно переложить на компьютер.
Таким образом, если на некоторой выборке измерены две переменные, которые коррелируют друг с другом, то, вычислив коэффициенты регрессии, мы получаем возможность предсказания неизвестных значений одной переменной (y – «зависимая переменная») по известным значениям другой переменной (x – «независимая переменная»).
Понятно, что наиболее точным предсказание будет, если | r xy| = 1. Тогда каждому значению x будет соответствовать только одно значение y, а все ошибки оценки будут равны 0 (все точки на графике рассеивания будут лежать на прямой регрессии).
Если же r xy = 0, то a1 = 0 и у i= a 0(= у ср), т. е. при любом x оценка переменной y будет равна ее среднему значению и предсказательная ценность регрессии ничтожна.
Следует отметить, что на коэффициент линейной корреляции влияют выбросы (экстремально большие или малые значения признака) так как величина этого коэффициента прямо пропорциональна отклонению значения переменной от среднего.
Способы борьбы с выбросами:
1) «чистка» данных. Можно для каждой переменной установить определенное ограничение на диапазон ее изменчивости. Например, исключаете наблюдения, которые выходят за пределы диапазона xcр±2σ или.xcр±3σ.
2) применение ранговых коэффициентов корреляции.
Основные причины обязательного присутствия в регрессионных моделях случайного отклонения следующие.
· Неполнота учета объясняющих переменных. Любая эконометрическая модель упрощает реальную ситуацию. Например, спрос на товар определяется его ценой, а также ценой на товары-заменители, ценой на дополняющие товары, доходом потребителей, их количеством, традициями, национальными особенностями, погодой и т.д. При этом заранее неизвестно, какими факторами можно пренебречь, а по некоторым невозможно получить данные.
· Неправильный выбор формулы уравнения регрессии. Для парной регрессии выбор формулы обычно осуществляется по графическому изображению статистических данных в виде точек в декартовой системе координат, которое называется диаграммой рассеивания.
·
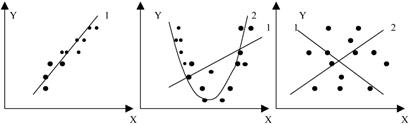
· Агрегирование переменных. Отдельные факторы могут оказаться сложной комбинацией более простых переменных.
· Ошибки измерений.
· Непредсказуемость человеческого фактора.
Довольно часто в исследованиях встречаются немонотонные связи — когда связь меняет свое направление (с прямого на обратное, или наоборот) при увеличении или уменьшении значений одной из переменной. Типичный пример —это связь уровня активации (X) и продуктивности деятельности (Y). Любой из рассмотренных коэффициентов корреляции будет в этом случае иметь значение, близкое к нулю.
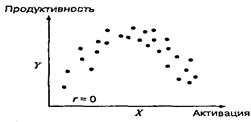
Если наблюдается немонотонная нелинейность связи, то можно сначала найти точку перегиба по графику рассеивания и разделить выборку на две группы, различающиеся направлением связи между переменными. После этого можно вычислять корреляции отдельно для каждой группы.
- Анализ статистической значимости коэффициентов линейной регрессии
Рассчитанные значения коэффициентов уравнения регрессии это случайные величины, дисперсии которых определяются следующими выражениями:
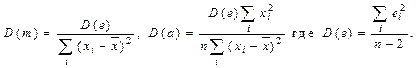
Здесь D (e) – необъясненная дисперсия зависимой переменной вокруг линии регрессии. Естественно, что вместе с ней растут и дисперсии коэффициентов уравнения регрессии. Из рисунка ясно, что при D (e) > 0 уменьшение диапазона изменения независимой переменной (сближение точек 1 и 3) приведет к возрастанию погрешности. Чем больше абсолютные значения x, тем сильнее изменится дисперсия свободного члена a при изменении наклона регрессионной прямой.
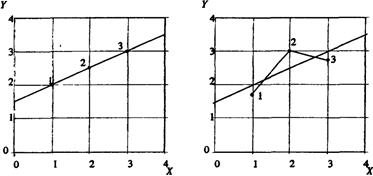
Формально значимость оцененного коэффициента регрессии a1 может быть проверена с помощью анализа его отношения к своему стандартному отклонению. Эта величина имеет t -распределение Стьюдента с (п-2) степенями свободы и называется t-статистикой. Можно использовать следующее грубое правило. Если стандартная ошибка коэффициента больше его модуля (t < 1), то он не может быть признан хорошим (значимым), поскольку доверительная вероятность здесь при двусторонней альтернативной гипотезе составляет лишь менее чем приблизительно 0, 7. Если стандартная ошибка меньше модуля коэффициента, но больше его половины (1 < t < 2), то сделанная оценка может рассматриваться как более или менее значимая. Доверительная вероятность будет примерно от 0, 7 до 0, 95. Значение t от 2 до 3 свидетельствует о весьма значимой связи. Конечно, с ростом числа наблюдений прочих равных условиях выводы о наличии связи становятся надежнее. Но уже для п порядка 10 и более сформулированные правила приблизительно верны.
- Коэффициент детерминации
Оказывается, что отношение дисперсии оценок зависимой переменной к ее истинной дисперсии равно квадрату коэффициента корреляции. Поэтому квадрат коэффициента корреляции, который представляет долю дисперсии зависимой переменной, обусловленной влиянием независимой переменной, называется коэффициентом детерминации.
Коэффициент детерминации обладает важным преимуществом по сравнению с коэффициентом корреляции. Корреляция не является линейной функцией связи между двумя переменными. Поэтому, в частности, среднее арифметическое коэффициентов корреляции для нескольких выборок не совпадает с корреляцией, вычисленной сразу для всех испытуемых из этих выборок. Напротив, коэффициент детерминации отражает связь линейно и поэтому является аддитивным: допускается его усреднение для нескольких выборок.
В отличие от коэффициента корреляциикоэффициент детерминации линейно возрастает с увеличением силы связи. На этом основании можно ввести три градации величин корреляции по силе связи:
r ≤ 0, 3 — слабая связь (менее 10% от общей доли дисперсии);
0, 3 < r ≤ 0, 7 — умеренная связь (от 10 до 50% от общей доли дисперсии);
r > 0, 7 — сильная связь (50% и более от общей доли дисперсии);
{
Коэффициент детерминации определяет на сколько процентов учтенные в корреляционной модели факторы объясняют изменение результативного показателя
| |||
| Модель устойчива, если D> 70% } |